Giải mục I trang 54,55,56 SGK Toán 7 tập 2 - Cánh diềua) Thực hiện phép cộng trong mỗi trường hợp sau b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
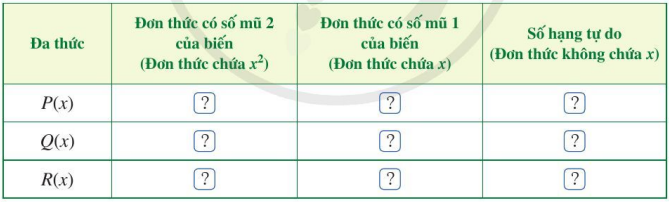
I. Cộng hai đa thức một biến HĐ 1 a) Thực hiện phép cộng trong mỗi trường hợp sau: \(5{x^2} + 7{x^2}\); \(a{x^2} + b{x^2}\) (k \(\in\) N*). b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến. Phương pháp giải: a) Để thực hiện phép cộng trong các phép tính, ta giữ nguyên biến và cộng các hệ số lại với nhau. b) Rút ra quy tắc cộng hai đơn thức có cùng số mũ của biến từ cách thực hiện phần a. Lời giải chi tiết: a) \(5{x^2} + 7{x^2} = (5 + 7){x^2} = 12{x^2}\); \(a{x^2} + b{x^2} = (a + b){x^2}\). b) Muốn cộng hai đơn thức có cùng số mũ của biến, ta giữ nguyên biến và tính tổng của các hệ số có trong đơn thức. HĐ 2 Cho hai đa thức \(P(x) = 5{x^2} + 4 + 2x\) và \(Q(x) = 8x + {x^2} + 1\). a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến. b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức R(x). Phương pháp giải: a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng. c) Xác định đơn thức R(x) dựa vào kết quả phần b). Lời giải chi tiết: a) \(P(x) = 5{x^2} + 4 + 2x = 5{x^2} + 2x + 4\); \(Q(x) = 8x + {x^2} + 1 = {x^2} + 8x + 1\). b)
c) Vậy \(R(x) = 6{x^2} + 10x + 5\). LT - VD 1 Để cộng hai đa thức P(x), Q(x), bạn Dũng viết như dưới đây có đúng không? Vì sao? Nếu chưa đúng, em hãy sửa lại cho đúng. Phương pháp giải: Xem lại cách thức cộng hai đơn thức theo hàng dọc: - Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến; - Đặt hai đơn thức có cùng số mũ của biến ở cùng cột; - Cộng hai đơn thức trong từng cột, ta có tổng cần tìm. Và xem lại Ví dụ 2. Lời giải chi tiết: Cách làm của bạn Dũng chưa đúng. Lí do: + Vì các đơn thức 3x và 6 không có cùng số mũ của biến nên chúng không được viết ở cùng cột. + Vì các đơn thức – 1 và 2x không có cùng số mũ của biến nên chúng không được viết ở cùng cột. Các đơn thức 3x và 2x sẽ được viết cùng cột (cùng có số mũ của biến là 1); các đơn thức 6 và – 1 sẽ được viết cùng cột (cùng số mũ của biến là 0). Cách viết đúng là: HĐ 3 Cho hai đa thức: \(P(x) = - 2{x^2} + 1 + 3x\) và \(Q(x) = - 5x + 3{x^2} + 4\). a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến. b) Viết tổng P(x) + Q(x) theo hàng ngang. c) Nhóm các đơn thức có cùng số mũ của biến với nhau. d) Tính tổng P(x) + Q(x) bằng cách thực hiện phép tính trong từng nhóm. Phương pháp giải: a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. (Ở cả 2 đa thức đã cho thì số mũ lớn nhất là 2 rồi đến 1 và 0). b) Viết tổng hai đa thức theo hàng ngang. c) Nhóm các đơn thức có cùng số mũ của biến với nhau. d) Thực hiện phép tính sau khi đã nhóm. Lời giải chi tiết: a) \(P(x) = - 2{x^2} + 1 + 3x = - 2{x^2} + 3x + 1\); \(Q(x) = - 5x + 3{x^2} + 4 = 3{x^2} - 5x + 4\). b) \(P(x) + Q(x) = ( - 2{x^2} + 3x + 1) + (3{x^2} - 5x + 4)\). c) \(\begin{array}{l}P(x) + Q(x) = ( - 2{x^2} + 3x + 1) + (3{x^2} - 5x + 4)\\ = - 2{x^2} + 3x + 1 + 3{x^2} - 5x + 4\\ = ( - 2{x^2} + 3{x^2}) + (3x - 5x) + (1 + 4)\end{array}\) d) \(\begin{array}{l}P(x) + Q(x) = ( - 2{x^2} + 3{x^2}) + (3x - 5x) + (1 + 4)\\ = ( - 2 + 3){x^2} + (3 - 5)x + (1 + 4)\\ = {x^2} - 2x + 5\end{array}\) LT - VD 2 Tính tổng của hai đa thức sau bằng hai cách: \(P(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2\); \(Q(x) = - 8{x^3} + 4{x^2} + 6 + 3x\). Phương pháp giải: Nhớ lại cách thức cộng hai đa thức theo cột dọc và theo hàng ngang: Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau: - Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến; - Đặt hai đơn thức có cùng số mũ của biến ở cùng cột; - Cộng hai đơn thức trong từng cột, ta có tổng cần tìm. Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau: - Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến; - Viết tổng hai đơn thức theo hàng ngang; - Nhóm các đơn thức có cùng số mũ của biến với nhau; - Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm. Lời giải chi tiết: Theo cột dọc: Theo hàng ngang: \(\begin{array}{l}P(x) + Q(x) = 2{x^3} + \dfrac{3}{2}{x^2} + 5x - 2 + ( - 8){x^3} + 4{x^2} + 3x + 6\\ = (2 - 8){x^3} + (\dfrac{3}{2} + 4){x^2} + (5 + 3)x + ( - 2 + 6)\\ = - 6{x^3} + \dfrac{{11}}{2}{x^2} + 8x + 4\end{array}\)
|














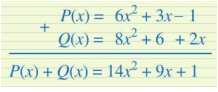
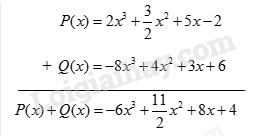






Danh sách bình luận