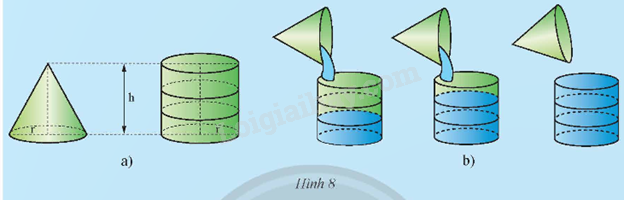
Giải mục 3 trang 91 SGK Toán 9 tập 2 - Chân trời sáng tạoLấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h: a) Thể tích của bình hình trụ; b) Thể tích của gàu hình nón. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 91 SGK Toán 9 Chân trời sáng tạo Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h: a) Thể tích của bình hình trụ; b) Thể tích của gàu hình nón.
Phương pháp giải: - Thể tích của hình trụ là: \(V = \pi {r^2}h\) - Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón). Lời giải chi tiết: a) Thể tích của bình hình trụ là: \(V = \pi {r^2}h\) b) Thể tích của gàu hình nón là: \(V' = \frac{V}{3} = \frac{{\pi {r^2}h}}{3}\). TH4 Video hướng dẫn giải Trả lời câu hỏi Thực hành 4 trang 91 SGK Toán 9 Chân trời sáng tạo Tính thể tích của hình nón có bán kính đáy 6 cm, chiều cao 4 cm. Phương pháp giải: Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón). Lời giải chi tiết: Thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.4 = 48\pi \) (cm3). VD Video hướng dẫn giải Trả lời câu hỏi Vận dụng trang 91 SGK Toán 9 Chân trời sáng tạo Từ một khối gỗ có dạng hình lập phương cạnh 6 cm, người ta khoét một hình nón có đường kính mặt đáy là 4 cm và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (Hình 10). Hãy tính thể tích của phần khối gỗ còn lại (kết quả làm tròn đến hàng đơn vị).
Phương pháp giải: Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón). Lời giải chi tiết: Thể tích khối lập phương là: V = 63 = 216 (cm3). Thể tích hình nón là: \(V' = \frac{1}{3}.\pi {r^2}h = \frac{1}{3}.\pi {\left( {\frac{4}{2}} \right)^2}.6 = 8\pi \) (cm3). Thể tích khối gỗ còn lại là: V – V’ = 216 – 8\(\pi \) = 191 (cm3).
|





















Danh sách bình luận