Giải mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo

TH4

Trả lời câu hỏi Thực hành 4 trang 65 SGK Toán 9 Chân trời sáng tạo

a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):

22^o

52^o

15^o20’

52^o18’

b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):

sin x = 0,723

cos y = 0,828

tan z = 3,77

cot t = 1,54.

Phương pháp giải:

-  Dựa vào VD4 trang 64 làm tương tự.

-  Dựa vào VD5 trang 65 làm tương tự.

Lời giải chi tiết:

a) \(\sin {52^o} \approx 0,375;\cos {22^o} \approx 0,927;\tan {22^o} \approx 0,404;\cot {22^o} \approx 2,745\)

\(\sin {52^o} \approx 0,788;\cos {52^o} \approx 0,616;\tan {52^o} \approx 1,28;\cot {52^o} \approx 0,781\)

\(\sin {15^o20’} \approx 0,264;\cos {15^o20’} \approx 0,964;\tan {15^o20’} \approx 0,274;\cot {15^o20’} \approx 3,647\)

\(\sin {52^o18’} \approx 0,791;\cos {52^o18’} \approx 0,612;\tan {52^o18’} \approx 1,294;\cot {52^o18’}  \approx 0,773\)

b) Góc x \( \approx {46^o}18'\)

góc y \( \approx {34^o}6'\)

góc z \( \approx {75^o}8'\)

góc t \( \approx {32^o}59'\) 

VD4

Trả lời câu hỏi Vận dụng 4 trang 65 SGK Toán 9 Chân trời sáng tạo

a) Vẽ một tam giác vuông có góc bằng 40^o . Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40^o . Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.

b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thức đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.

Phương pháp giải:

Đọc kĩ dữ liệu đầu bài để vẽ hình, sử dụng:

+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).

+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).

+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).

+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).

Lời giải chi tiết:

a)

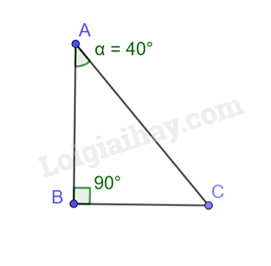
Các tỉ số lượng giác của góc \(\alpha \) là:

sin \(\alpha \) = \(\frac{{BC}}{{AC}} \approx 0,64\)

cos \(\alpha \) = \(\frac{{AB}}{{AC}} \approx 0,77\)

tan \(\alpha \) = \(\frac{{BC}}{{AB}} \approx 0,84\)

cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} \approx 1,19\)

b)

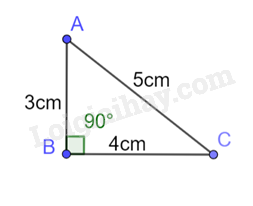
Các tỉ số lượng giác của góc \(\widehat {BAC}\) là:

sin \(\widehat {BAC}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)

cos \(\widehat {BAC}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)

tan \(\widehat {BAC}\) = \(\frac{{BC}}{{AB}} = \frac{4}{3}\)

cot \(\widehat {BAC}\) = \(\frac{1}{{\tan \alpha }} = \frac{3}{4}\)

Các tỉ số lượng giác của góc \(\widehat {ACB}\) là:

sin \(\widehat {ACB}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)

cos \(\widehat {ACB}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)

tan \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{3}{4}\)

cot \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {BAC}}} = \frac{4}{3}\) 

Sử dụng thước đo góc, ta đo được \(\widehat {BAC} \approx 53^\circ\) và \(\widehat {ACB} \approx 37^\circ\). Kiểm tra lại các tỉ số lượng giác bằng máy tính cầm tay, ta thấy các giá trị bằng với giá trị mình viết phía trên.