Giải mục 2 trang 9, 10, 11, 12, 13, 14 SGK Toán 11 tập 1 - Cánh DiềuHoạt động 6: a) Trong mặt phẳng tọa độ ( định hướng) Oxy, hãy vẽ đường tròn tâm O với bán kính bằng 1. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
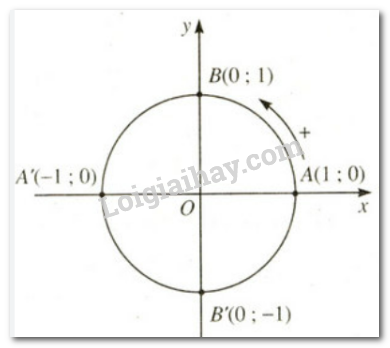
HĐ6 Trả lời câu hỏi Hoạt động 6 trang 10 SGK Toán 11 Cánh diều a) Trong mặt phẳng tọa độ (định hướng) Oxy, hãy vẽ đường tròn tâm O và bán kính bằng 1. b) Hãy nêu chiều dương, chiều âm trên đường tròn tâm O với bán kính bằng 1. Phương pháp giải: Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ hình. Lời giải chi tiết: a)
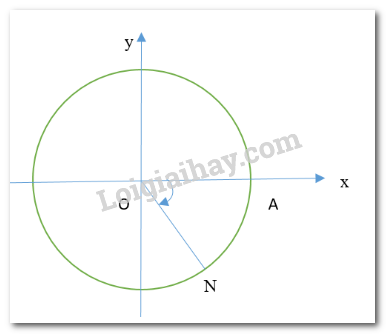
b) Chiều dương là chiều ngược chiều kim đồng hồ. Chiều âm là chiều kim đồng hồ. LT-VD6 Trả lời câu hỏi Luyện tập - Vận dụng 6 trang 10 SGK Toán 11 Cánh diều Xác định điểm N trên đường tròn lượng giác sao cho \(\left( {OA,ON} \right) = - \frac{\pi }{3}\). Phương pháp giải: Dựa vào kiến thực đã học về trục tọa độ và kiến thức học ở phần trên để xác vẽ. Lời giải chi tiết:
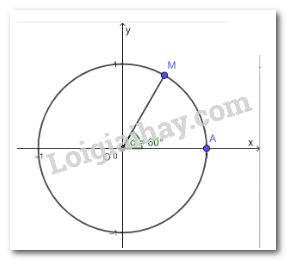
HĐ7 Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 11 Cánh diều a) Xác định điểm M trên đường tròn lượng giác sao cho \(\left( {OA,OM} \right) = 60^\circ \). b) So sánh hoành độ của điểm M với \(\cos 60^\circ \); tung độ của điểm M với \(\sin 60^\circ \). Phương pháp giải: Dựa vào cách xác định góc bên trên để xác định. Lời giải chi tiết: a)
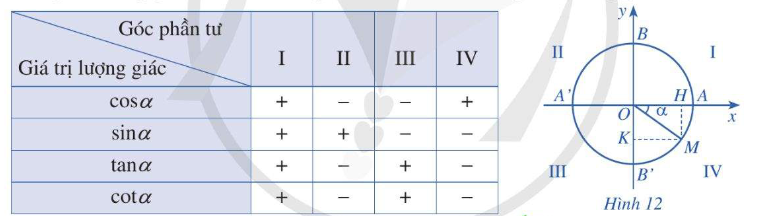
b) \(\cos 60^\circ \) bằng hoành độ của điểm M, \(\sin 60^\circ \) bằng tung độ của điểm M. LT-VD7 Trả lời câu hỏi Luyện tập - Vận dụng 7 trang 11 SGK Toán 11 Cánh diều Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\). Phương pháp giải: Dựa vào kiến thức đã học để tính. Lời giải chi tiết: \(\sin \left( { - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2};\,\,\cos \left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( { - \frac{\pi }{4}} \right) = - \frac{1}{2};\,\,\cot \left( { - \frac{\pi }{4}} \right) = - 2\) HĐ8 Trả lời câu hỏi Hoạt động 8 trang 11 SGK Toán 11 Cánh diều Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \). Phương pháp giải: Dựa vào sin, cos, tan, cot đã học ở lớp dưới để xác định. Lời giải chi tiết: \(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\) LT-VD8 Trả lời câu hỏi Luyện tập - Vận dụng 8 trang 11 SGK Toán 11 Cánh diều Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\). Phương pháp giải: Dựa vào bảng xét dấu sau:
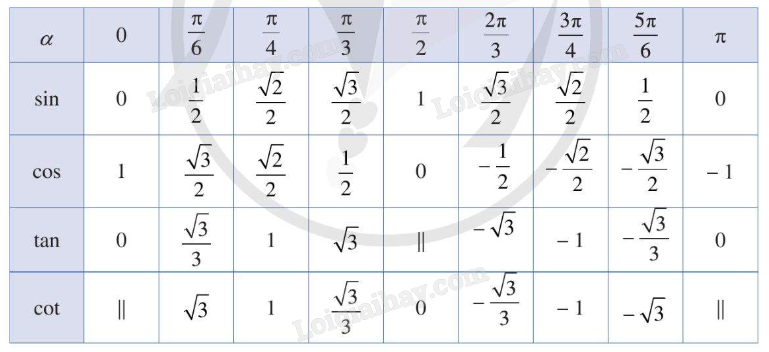
Lời giải chi tiết: Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên: \(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\) HĐ9 Trả lời câu hỏi Hoạt động 9 trang 11 SGK Toán 11 Cánh diều Cho góc lượng giác \(\alpha \). So sánh: a) \({\cos ^2}\alpha + {\sin ^2}\alpha \) và 1; b) \(\tan \alpha .\cot \alpha \) và 1 với \(\cos \alpha \ne 0,\,\sin \alpha \ne 0\); c) \(1 + {\tan ^2}\alpha \) và \(\frac{1}{{{{\cos }^2}\alpha }}\) với \(\cos \alpha \ne 0\); d) \(1 + {\cot ^2}\alpha \) và \(\frac{1}{{{{\sin }^2}\alpha }}\) với \(\sin \alpha \ne 0\). Phương pháp giải: Dựa vào kiến thức của phần phía trên và kiến thức lớp 9 để so sánh. Lời giải chi tiết: a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\). b) \(\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\). c) \(\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\). d) \(\frac{1}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \). LT-VD9 Trả lời câu hỏi Luyện tập - Vận dụng 9 trang 12 SGK Toán 11 Cánh diều Cho góc lượng giác \(\alpha \) sao cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = - \frac{4}{5}\). Tìm \(\cos \alpha \). Phương pháp giải: Sử dụng công thức lượng giác \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\). Lời giải chi tiết: Vì \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\) nên \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{4}{5}} \right)^2} = \frac{9}{{25}}\). Do \(\pi < \alpha < \frac{{3\pi }}{2}\) nên \(\cos \alpha < 0\). Suy ra \(\cos \alpha = - \frac{3}{5}\). HĐ10 Trả lời câu hỏi Hoạt động 10 trang 12 SGK Toán 11 Cánh diều Tìm các giá trị lượng giác của góc lượng giác \(\alpha = \frac{\pi }{4}\). Phương pháp giải: Dựa vào các kiến thức đã học để tính. Lời giải chi tiết: \(\sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\,\,\cos \left( {\frac{\pi }{4} } \right) = \frac{{\sqrt 2 }}{2};\,\,\tan \left( {\frac{\pi }{4} } \right) = 1;\,\,\cot \left( {\frac{\pi }{4} } \right) = 1\). LT-VD10 Trả lời câu hỏi Luyện tập - Vận dụng 10 trang 12 SGK Toán 11 Cánh diều Tính giá trị của biểu thức: \(Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\). Phương pháp giải: Sử dựng bảng lượng giác của các góc đặc biệt:
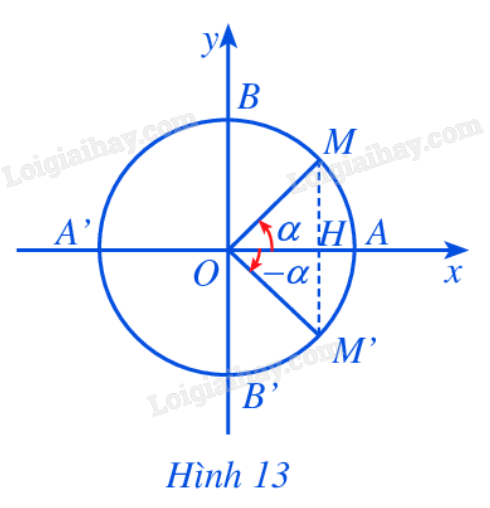
Lời giải chi tiết: Ta có: \(\begin{array}{l}Q = {\tan ^2}\frac{\pi }{3} + {\sin ^2}\frac{\pi }{4} + \cot \frac{\pi }{4} + \cos \frac{\pi }{2}\\={\left( {\sqrt 3 } \right)^2} + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + 1 + 0 = \frac{7}{2}.\end{array}\) HĐ11 Trả lời câu hỏi Hoạt động 11 trang 13 SGK Toán 11 Cánh diều Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha\), \(\left( {OA,OM'} \right) = - \alpha \) (Hình 13).
a) Nêu nhận xét về: hoành độ của chúng, tung độ của hai điểm M, M'. b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \) và \(- \alpha \). Phương pháp giải: Dựa vào hình vẽ (Hình 13). Lời giải chi tiết: a) Hoành độ của điểm M và M’ bằng nhau. Tung độ của điểm M và M’ đối nhau. b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha\) và \(- \alpha \).
LT-VD11 Trả lời câu hỏi Luyện tập - Vận dụng 11 trang 14 SGK Toán 11 Cánh diều Tính: a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8}\). b) \(\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\). Phương pháp giải: Sử dụng công thức trong bảng:
Lời giải chi tiết: a) \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} = {\cos ^2}\frac{\pi }{8} + {\cos ^2}\left( {\frac{\pi }{2} - \frac{\pi }{8}} \right)\) \(= {\cos ^2}\frac{\pi }{8} + {\sin ^2}\frac{\pi }{8} = 1\). b) \(\begin{array}{l}\tan {1^ \circ }.\tan {2^ \circ }.\tan {45^ \circ }.\tan {88^ \circ }.\tan {89^ \circ }\\ = (\tan {1^ \circ }.\tan {89^ \circ }).(\tan {2^ \circ }.\tan {88^ \circ }).\tan {45^ \circ }\\ = (\tan {1^ \circ }.\cot {1^ \circ }).(\tan {2^ \circ }.\cot {2^ \circ }).\tan {45^ \circ }\\ = 1.\end{array}\) LT-VD12 Trả lời câu hỏi Luyện tập - Vận dụng 12 trang 12 SGK Toán 11 Cánh diều Dùng máy tính cầm tay để tính: a) \(\tan ( - {75^ \circ })\); b) \(\cot \left( { - \frac{\pi }{5}} \right)\). Phương pháp giải: Sử dụng máy tính cầm tay. Lời giải chi tiết: a) \(\tan ( - {75^ \circ }) = - 2 - \sqrt 3 \). b) \(\cot \left( { - \frac{\pi }{5}} \right) \approx - 1,376\).
|






















Danh sách bình luận