Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều

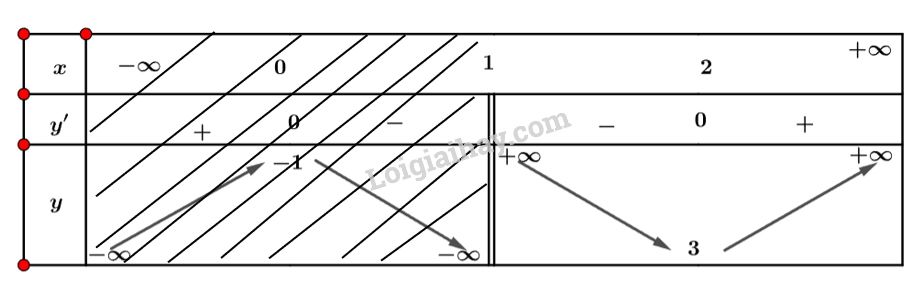
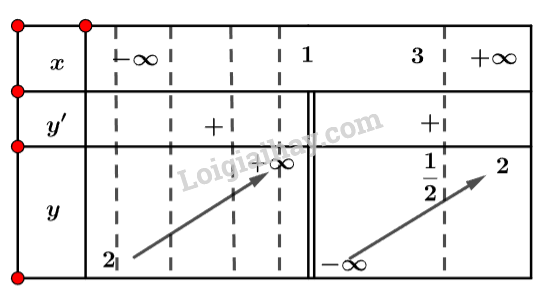
HĐ2

Trả lời câu hỏi Hoạt động 2 trang 16 SGK Toán 12 Cánh diều

Cho hàm số \(f\left( x \right) = x + \frac{1}{{x - 1}}\) với \(x > 1\).

a) Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right)\).

b) Lập bảng biến thiên của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(f\left( x \right)\) trên khoảng \(\left( {1; + \infty } \right)\).

Phương pháp giải:

a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) =  + \infty \\\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  + \infty \end{array} \right.\)

b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:

c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.

Lời giải chi tiết:

a) Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) =  + \infty \\\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  + \infty \end{array} \right.\)

b) Bảng biến thiên của hàm số trên khoảng \(\left( {1; + \infty } \right)\) là:

c) Hàm số có giá trị nhỏ nhất bằng 3 khi \(x = 2\) và không có giá trị lớn nhất.

LT2

Trả lời câu hỏi Luyện tập 2 trang 16 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{{2x - 5}}{{x - 1}}\) trên nửa khoảng \((1;3]\).

Phương pháp giải:

B1: Tìm tập xác định của hàm số.

B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.

B3: Lập bảng biến thiên của hàm số.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải chi tiết:

Ta có: \(y' = \frac{3}{{{{\left( {x - 1} \right)}^2}}}\).

Nhận xét \(y' > 0{\rm{ }}\forall x \in D\).

Ta có bảng biến thiên:

Vậy hàm số có giá trị lớn nhất bằng \(\frac{1}{2}\) khi \(x = 3\) và không có giá trị nhỏ nhất.

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 17 SGK Toán 12 Cánh diều

Cho hàm số \(y = f\left( x \right) = 2{x^3} - 6x,x \in \left[ { - 2;2} \right]\) có đồ thị là đường cong ở Hình 9.

a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.

b) Giải phương trình \(f'\left( x \right) = 0\) với \(x \in \left( { - 2;2} \right)\)

c) Tính các giá trị của hàm số \(f\left( x \right)\) tại hai đầu mút \( - 2;2\) và tại các điểm \(x \in \left( { - 2;2} \right)\) mà ở đó \(f'\left( x \right) = 0\)

d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Lời giải chi tiết:

a) Ta có: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 4\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) =  - 4\end{array} \right.\).

b) Ta có: \(f'\left( x \right) = 6{x^2} - 6\).

Xét \(f'\left( x \right) = 0 \Leftrightarrow x =  \pm 1\).

c) Ta có:\(\left\{ \begin{array}{l}f\left( 2 \right) = f\left( { - 1} \right) = 4\\f\left( { - 2} \right) = f\left( 1 \right) =  - 4\end{array} \right.\).

d) Nhận xét: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( 2 \right) = f\left( { - 1} \right)\\\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = f\left( { - 2} \right) = f\left( 1 \right)\end{array} \right.\).

LT3

Trả lời câu hỏi Luyện tập 3 trang 18 SGK Toán 12 Cánh diều

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \sin 2x - 2x\) trên đoạn \(\left[ {\frac{\pi }{2};\frac{{3\pi }}{2}} \right]\).

Phương pháp giải:

B1: Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.

B2: Tính \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),f\left( a \right),f\left( b \right)\)

B3: So sánh các giá trị tìm được ở bước 2 và kết luận

Lời giải chi tiết:

Ta có: \(f'\left( x \right) = 2\cos 2x - 2\).

Xét \(f'\left( x \right) = 0 \Leftrightarrow x = \pi \).

Ta có \(f\left( {\frac{\pi }{2}} \right) =  - \pi ,f\left( \pi  \right) =  - 2\pi ,f\left( {\frac{{3\pi }}{2}} \right) =  - 3\pi \)

Vậy hàm số \(f\left( x \right) = \sin 2x - 2x\) có giá trị nhỏ nhất bằng \( - 3\pi \) khi \(x = \frac{{3\pi }}{2}\) và có giá trị lớn nhất bằng \( - \pi \) khi \(x = \frac{\pi }{2}\) .