Giải mục 2 trang 15, 16, 17 Chuyên đề học tập Toán 10 - Chân trời sáng tạoMột nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
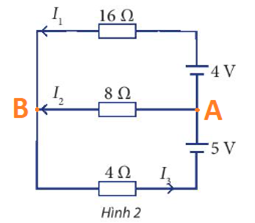
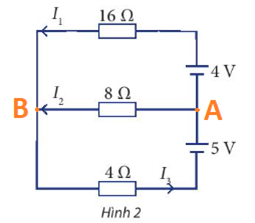
Thực hành 2 Một nhà hóa học có ba dung dịch cùng một loại acid nhưng với nồng độ khác nhau là 10%, 20% và 40%. Trong một thí nghiệm, để tạo ra 100ml dung dịch nồng độ 18%, nhà hóa học đã sử dụng lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40%. Tính số mililit dung dịch mỗi loại mà nhà hóa học đó đã sử dụng trong thí nghiệm này. Phương pháp giải: Bước 1: Lập hệ phương trình + Chọn ẩn và đặt điều kiện cho ẩn + Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết + Lập các phương trình biểu thị mối quan hệ giữa các đại lượng Bước 2: Giải hệ phương trình Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận. Lời giải chi tiết: Gọi số mililit dung dịch mỗi loại 10%, 20% và 40% sử dụng trong thí nghiệm là x, y, z (đơn vị mililit) \((x,y,z > 0)\) Tạo ra 100ml dung dịch mới nên ta có: \(x + y + z = 100\) Khối lượng chất tan trong dung dịch mới là: \(10\% x + 20\% y + 40\% z = 18\% .100 \Leftrightarrow 0,1x + 0,2y + 0,4z = 18\) Lượng dung dịch nồng độ 10% gấp bốn lần lượng dung dịch nồng độ 40% nên \(x = 4z\) Từ đó ta có hệ phương trình bậc nhất ba ẩn: \(\left\{ \begin{array}{l}x + y + z = 100\\0,1x + 0,2y + 0,4z = 18\\x - 4z = 0\end{array} \right.\) Sử dụng máy tính cầm tay, ta được \(x = 40;y = 50;z = 10\) Vậy nhà hóa học đó đã dùng 40ml dung dịch 10%, 50ml dung dịch 20%,10ml dung dịch 40%. Vận dụng 1 Ba loại tế bào A, B, C thực hiện số lần nguyên phân lần lượt là 3, 4, 7 và tổng số tế bào con tạo ra là 480. Biết rằng khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C. Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra. Tính số tế bào con mỗi loại lúc ban đầu. Phương pháp giải: Bước 1: Lập hệ phương trình + Chọn ẩn và đặt điều kiện cho ẩn + Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết + Lập các phương trình biểu thị mối quan hệ giữa các đại lượng Bước 2: Giải hệ phương trình Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận. Lời giải chi tiết: Gọi số tế bào con mỗi loại A, B, C lúc đầu là x, y, z (tế bào) \((x,y,z \in \mathbb{N})\) Tổng số tế bào con tạo ra là 480 tế bào nên \(x{.2^3} + y{.2^4} + z{.2^7} = 480\) Khi chưa thực hiện nguyên phân, số tế bào loại B bằng tổng số tế bào loại A và loại C nên \(y = x + z\) Sau khi thực hiện nguyên phân, tổng số tế bào con loại A và loại C được tạo ra gấp năm lần số tế bào con loại B được tạo ra nên \(x{.2^3} + z{.2^7} = 5y{.2^4}\) Từ đó ta có hệ phương trình bậc nhất ba ẩn: \(\left\{ \begin{array}{l}x{.2^3} + y{.2^4} + z{.2^7} = 480\\y = x + z\\x{.2^3} + z{.2^7} = 5y{.2^4}\end{array} \right.\) Sử dụng máy tính cầm tay, ta được \(x = 2;y = 5;z = 3\) Vậy ban đầu có 2 tế bào loại A, 5 tế bào loại B và 3 tế bào loại C. Vận dụng 2 Cho sơ đồ mạch điện như Hình 2. Tính các cường độ dòng điện \({I_1},{I_2},{I_3}\)
Phương pháp giải: Bước 1: Lập hệ phương trình + Chọn ẩn và đặt điều kiện cho ẩn + Biểu diễn các đại lượng chưa biết theo ẩn và đại lượng đã biết + Lập các phương trình biểu thị mối quan hệ giữa các đại lượng Bước 2: Giải hệ phương trình Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận. Lời giải chi tiết: Ta có: \(\left. \begin{array}{l}{U_{AB}} = - {E_1} + {I_1}{R_1} = - 4 + 16{I_1}\\{U_{AB}} = {I_2}{R_2} = 8{I_2}\\{U_{AB}} = {E_2} - {I_3}{R_3} = 5 - 4{I_3}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l} - 4 + 16{I_1} = 8{I_2}\\5 - 4{I_3} = 8{I_2}\end{array} \right.\) Tại nút B: \({I_1} + {I_2} = {I_3}\) Từ đó ta có hệ phương trình bậc nhất ba ẩn: \(\left\{ \begin{array}{l}16{I_1} - 8{I_2} = 4\\8{I_2} + 4{I_3} = 5\\{I_1} + {I_2} - {I_3} = 0\end{array} \right.\) Sử dụng máy tính cầm tay, ta được \({I_1} = \frac{{11}}{{28}},{I_2} = \frac{2}{7},{I_3} = \frac{{19}}{{28}}\) Vậy \({I_1} = \frac{{11}}{{28}}A,{I_2} = \frac{2}{7}A,{I_3} = \frac{{19}}{{28}}A\)
|




















Danh sách bình luận