Giải mục 1 trang 89, 90 SGK Toán 11 tập 2 - Cánh Diều

Hoạt động 1

Quan sát Hình 32 và cho biết:

a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào;

b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc nào.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

a) Vì \(MH \bot \left( P \right),O \in \left( P \right)\) nên hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng \(HO\)

b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc \(\widehat {MOH}\).

Luyện tập 1

Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc \({20^ \circ }\) và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).

Phương pháp giải:

Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải chi tiết:

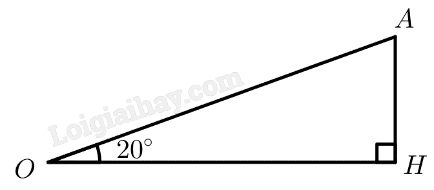
Đổi \(200km/h = \frac{{500}}{9}m/s\)

Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.

Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)

Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:

\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)

Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.