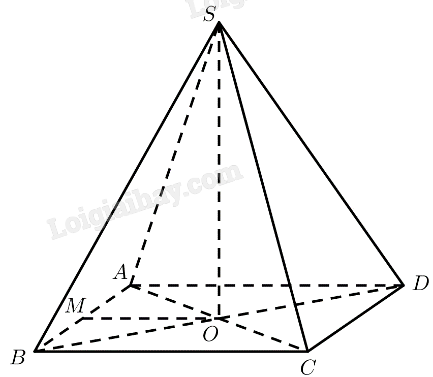
Bài 2 trang 94 SGK Toán 11 tập 2 - Cánh diều

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(O\), \(SO \bot \left( {ABCD} \right)\), tam giác \(SAC\) là tam giác đều.

a) Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\).

b) Chứng minh rằng \(AC \bot \left( {SBD} \right)\). Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).

c) Gọi \(M\) là trung điểm của cạnh \(AB\). Tính số đo của góc nhị diện \(\left[ {M,SO,D} \right]\).

Lời giải chi tiết

a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)

Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)

\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)

b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)

\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)

\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)

c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)

Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)

\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)

\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)

\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)

Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).