Giải mục 1 trang 39, 40 SGK Toán 11 tập 2 - Cánh Diều

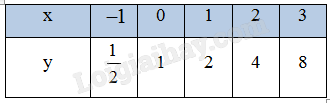
Hoạt động 1

Xét bài toán ở phần mở đầu.

a)     Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm

b)    Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm

Phương pháp giải:

Áp dụng kiến thức đã học để giải bài toán

Lời giải chi tiết:

a)     Số tiền doanh nghiệp đó có được

-         Sau 1 năm: \(1\,\,000\,\,000\,\,\,000 + 1\,\,000\,\,000\,\,\,000 \times 6,2\%  = 1\,\,062\,\,000\,\,\,000\) (đồng)

-         Sau 2 năm: \(1\,\,062\,\,000\,\,000 + 1\,\,062\,\,000\,\,000 \times 6,2\%  = 1\,\,127\,\,844\,\,000\) (đồng)

-         Sau 3 năm: \(1\,\,127\,\,844\,\,000 + 1\,\,127\,\,844\,\,000 \times 6,2\%  = 1\,\,197\,\,770\,\,328\) (đồng)

b)    Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm:

\(A = 1\,\,000\,\,000\,\,000 \times {\left( {1 + 6,2\% } \right)^n}\)

Luyện tập – Vận dụng 1

Cho hai ví dụ về hàm số mũ

Phương pháp giải:

Dựa vào định nghĩa hàm số mũ để cho ví dụ

Lời giải chi tiết:

\(y = {3^x};y = {5^{x + 3}}\)

Hoạt động 2

Cho hàm số mũ \(y = {2^x}\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

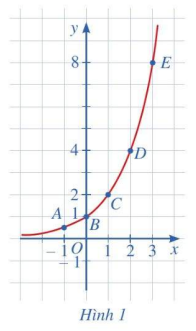
b)    Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.

Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)

c)     Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.

d)    Quan sát đồ thị hàm số \(y = {2^x}\), nêu nhận xét về:

• \(\mathop {\lim {2^x}}\limits_{x \to  + \infty } ;\,\mathop {\lim {2^x}}\limits_{x \to  - \infty } \)
• Sự biến thiên của hàm số \(y = {2^x}\) và lập bảng biến thiên của hàm số đó.

Phương pháp giải:

Áp dụng kiến thức đã học về giới hạn và lũy thừa để trả lời câu hỏi

Lời giải chi tiết:

a)     \(y = {2^x}\)

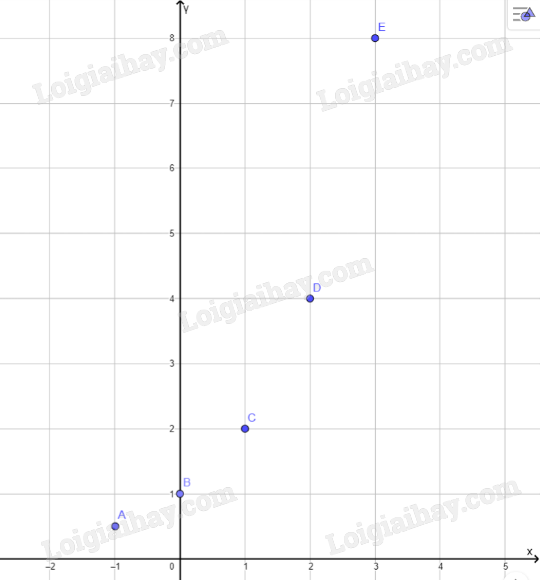
b)    Biểu diễn các điểm ở câu a:

c)     Tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung là (0;1)

Đồ thị hàm số đó không cắt trục hoành

d)    \(\mathop {\lim }\limits_{x \to  + \infty } {2^x} =  + \infty ;\,\,\mathop {\lim }\limits_{x \to  - \infty } {2^x} = 0\)

Hàm số \(y = {2^x}\) đồng biến trên toàn  \(\mathbb{R}\)

Bảng biến thiên của hàm số:

Hoạt động 3

Cho hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

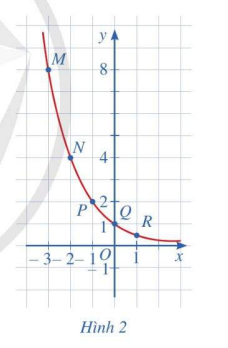
b,     Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.

Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{{\left( {\frac{1}{2}} \right)}^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) (Hình 2)

c,   Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.

d,     Quan sát đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), nêu nhận xét về:

• \(\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to  + \infty } ;\,\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to  - \infty } \)
• Sự biến thiên của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) và lập bảng biến thiên của hàm số đó.

Phương pháp giải:

Áp dụng kiến thức đã học về giới hạn và lũy thừa để trả lời câu hỏi

Lời giải chi tiết:

a)     \(y = {\left( {\frac{1}{2}} \right)^x}\)

a)     Biểu diễn các điểm ở câu a:

b)    Tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung là (0;1)

Đồ thị hàm số đó không cắt trục hoành

c)     \(\mathop {\lim }\limits_{x \to  + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to  - \infty } {\left( {\frac{1}{2}} \right)^x} =  + \infty \)

Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn  \(\mathbb{R}\)

Bảng biến thiên của hàm số:

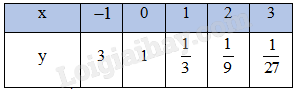
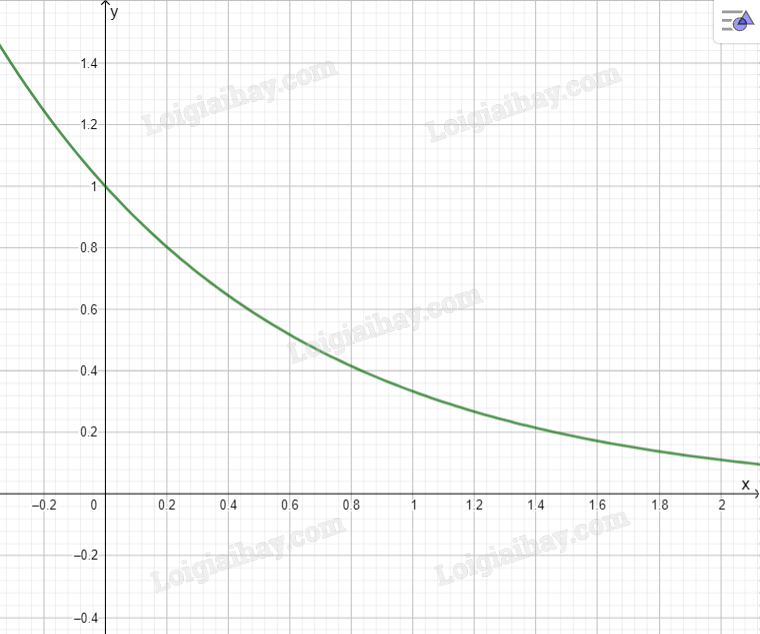
Luyện tập – Vận dụng 2

Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\)

Phương pháp giải:

Dựa vào đồ thị và bảng biến thiên của \(y = {\left( {\frac{1}{2}} \right)^x}\) để vẽ

Lời giải chi tiết:

\(\mathop {\lim }\limits_{x \to  + \infty } {\left( {\frac{1}{3}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to  - \infty } {\left( {\frac{1}{3}} \right)^x} =  + \infty \)

Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) nghịch biến trên toàn R

Bảng biến thiên của hàm số:

Đồ thị hàm số: