Giải mục 1 trang 22, 23, 24 SGK Toán 11 tập 1 - Cánh Diều

HĐ 1

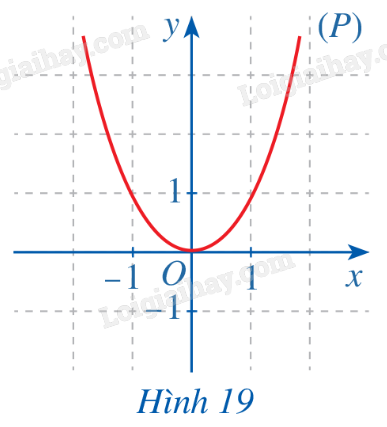
a)     Cho hàm số \(f\left( x \right) = {x^2}\)

Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { - x} \right)\) và \(f\left( x \right)\)

Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?

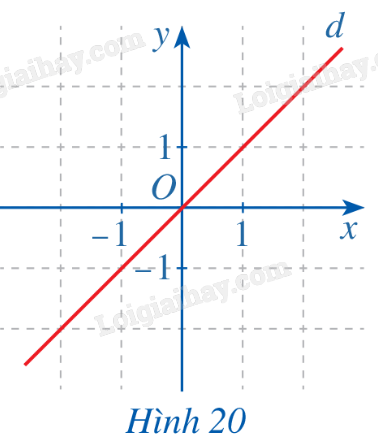
b)     Cho hàm số \(g\left( x \right) = x\)

Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { - x} \right)\) và \(g\left( x \right)\)

Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.

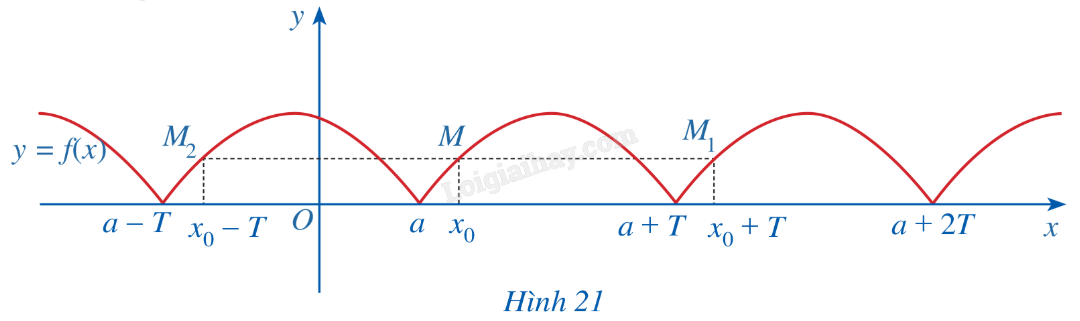
Phương pháp giải:

Dựa vào kiến thức về hàm số để xác định

Lời giải chi tiết:

a) 

Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)

Trục đối xứng của (P) là đường thẳng y = 0

b)    

Ta có: \(g\left( { - x} \right) =  - g\left( x \right)\)

Gốc tọa độ O là tâm đối xứng của đường thẳng d

LT - VD 1

a)     Chứng tỏ rằng hàm số \(g(x) = {x^3}\)là hàm số lẻ.

b)     Cho ví dụ về hàm số không là hàm số chẵn cũng không là hàm số lẻ.

Phương pháp giải:

Sử dụng định nghĩa hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:

a)    

Hàm số \(g(x) = {x^3}\)

+) Có tập xác định D = R;

+) Với mọi \(x \in R\)thì  \( - x \in R\)

Ta có \(g( - x) = {\left( { - x} \right)^3} =  - {x^3} =  - g(x)\)

Vậy \(g(x) = {x^3}\)là hàm số lẻ.

b)    

Ví dụ về hàm số không là hàm số chẵn không là hàm số lẻ là

\(f(x) = {x^3} + {x^2}\)

HĐ 2

Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.

a)     Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?

b)     Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)

Phương pháp giải:

Dựa vào cách nhìn đồ thị để trả lời câu hỏi

Lời giải chi tiết:

a)     Đồ thị hàm số trên mỗi đoạn là như nhau

b)     \(f\left( {{x_0} + T} \right) = f\left( {{x_0} - T} \right) = f\left( {{x_0}} \right)\)

LT - VD 2

Cho ví dụ về hàm số tuần hoàn

Phương pháp giải:

Sử dụng định nghĩa về hàm số tuần hoàn.

Lời giải chi tiết:

Ví dụ về hàm số tuần hoàn là : \(g(x) = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,,x \in Q\\1\,\,\,\,\,\,\,\,,x \in R\end{array} \right.\)