Giải mục 5 trang 29, 30 SGK Toán 11 tập 1 - Cánh DiềuXét tập hợp (E = Rbackslash left{ {kpi |k in mathbb{Z}} right}). Với mỗi số thực (x in E), hãy nêu định nghĩ (cot x) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ12 Trả lời câu hỏi Hoạt động 12 trang 29 SGK Toán 11 Cánh diều Xét tập hợp \(E = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\). Với mỗi số thực \(x \in E\), hãy nêu định nghĩa \(\cot x\). Phương pháp giải: Sử dụng công thức tính \(\cot x\). Lời giải chi tiết: \(\cot x = \frac{{\cos x}}{{\sin x}}\). HĐ13 Trả lời câu hỏi Hoạt động 13 trang 29 SGK Toán 11 Cánh diều Cho hàm số \(y = \cot x\). a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
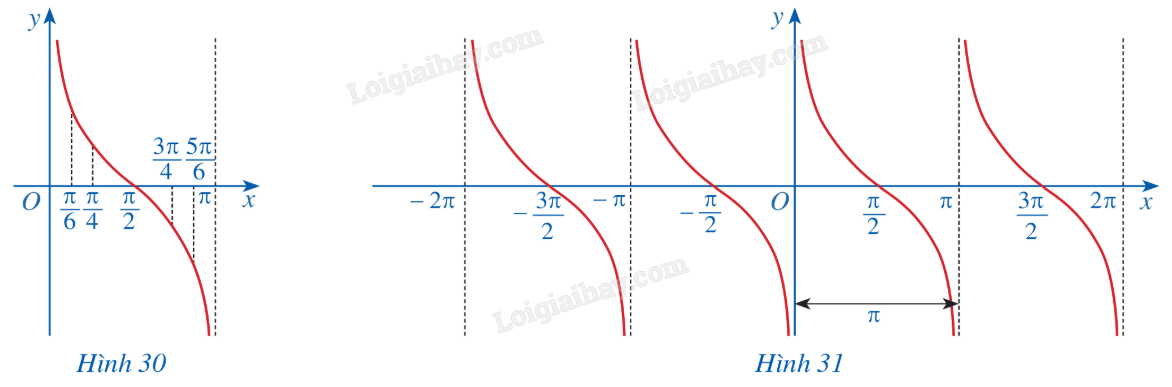
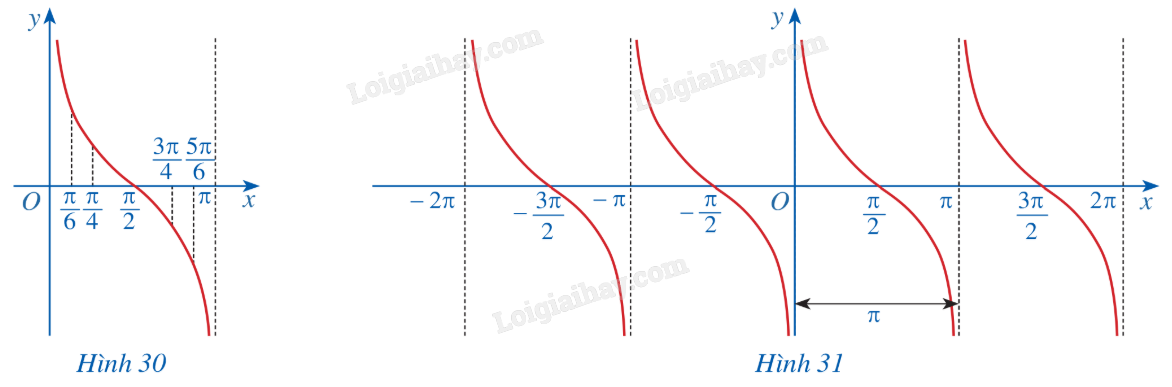
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 30). c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\) ta có đồ thị hàm số \(y = \cot x\) trên E được biểu diễn ở Hình 31.
Phương pháp giải: Sử dụng công thức tính cotang. Lời giải chi tiết: a)
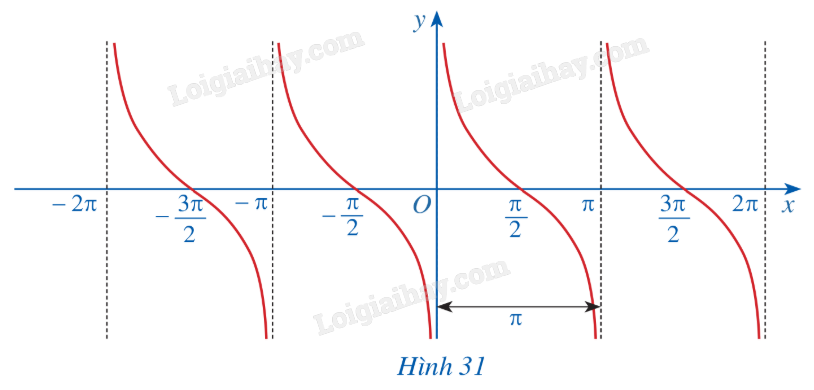
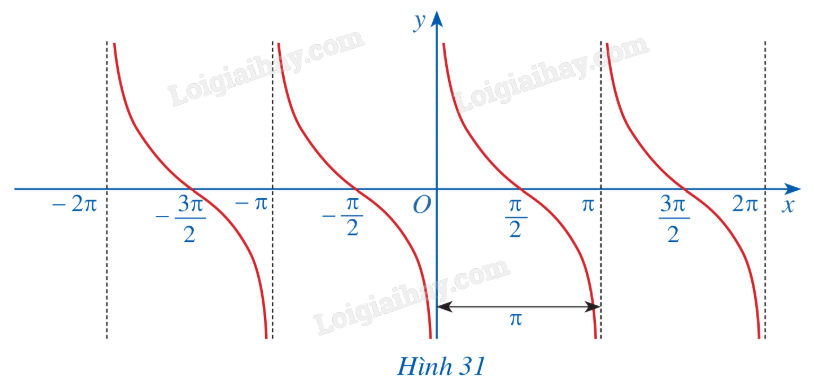
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; cotx) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) (Hình 30). c) Làm tương tự như trên đối với các khoảng \(\left( {\pi ;2\pi } \right),\left( { - \pi ;0} \right),\left( { - 2\pi ; - \pi } \right),....\) ta có đồ thị hàm số \(y = \cot x\) trên E được biểu diễn ở Hình 31.
HĐ14 Trả lời câu hỏi Hoạt động 14 trang 30 SGK Toán 11 Cánh diều Quan sát đồ thị hàm số \(y = \cot x\) ở Hình 31.
a) Nêu tập giá trị của hàm số \(y = \cot x\). b) Gốc tọa độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cot x\). c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\) hay không? Hàm số \(y = \cot x\) có tuần hoàn hay không? d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cot x\). Phương pháp giải: Sử dụng định nghĩa về hàm số cotang. Lời giải chi tiết: a) Tập giá trị của hàm số \(y = \cot x\) là R. b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số. Hàm số \(y = \cot x\) là hàm số lẻ. c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\). Hàm số \(y = \cot x\) có tuần hoàn. d) Hàm số \(y = \cot x\) nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\). LT-VD6 Trả lời câu hỏi Luyện tập - Vận dụng 6 trang 30 SGK Toán 11 Cánh diều Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m với đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\). Phương pháp giải: Sử dụng đồ thị của hàm số \(y = \cot x\). Lời giải chi tiết:
Theo đồ thì của hàm số \(y = \tan x\), số giao điểm của đường thẳng y = m với đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) là 1.
|




















Danh sách bình luận