Đề kiểm tra 45 phút chương 2 phần Đại số 7 - Đề số 1

Đề bài

Câu 1 ( 3 điểm)

1. (1 điểm) Hãy điền vào những từ còn thiếu trong câu sau:

a) Nếu hai đại lượng tỉ lệ thuận với nhau thì tỉ số hai giá trị tương ứng …

b) Nếu hai đại lượng tỉ lệ nghịch với nhau thì tích hai giá trị tương ứng …

2. (2 điểm) Cho ba số \(x, y, z\) biết rằng chúng tỉ lệ với \(3;5;7\) và \(y-x=10.\)

Hãy khoanh tròn vào chữ cái trước kết quả đúng.

\(\begin{array}{l}(A)\,15;21;27\\(B)\,15;25;35\\(C)\,17;25;35\\(D)\,17;25;35\end{array}\)

Câu 2 (3,5 điểm) Chia số \(635\) thành ba phần tỉ lệ nghịch với \(4;7\) và \(9.\) Hãy tìm ba phần đó.

Câu 3 (3,5 điểm) Cho hàm số \(y = 3x - 0,5\) .

a) (2 điểm) Hãy xác định các điểm sau đây có thuộc đồ thị của hàm số không:

\(A\left( {0; - 0,5} \right);\,B\left( {1;4} \right);\,C\left( { - 1; - 5} \right);\,D\left( { - 0,5; - 2} \right)\) .

b) (1,5 điểm) Vẽ đồ thị của hàm số.

Lời giải chi tiết

1.

Phương pháp:

Sử dụng lí thuyết đại lượng tỉ lệ thuận.

Sử dụng lí thuyết đại lượng tỉ lệ nghịch.

Lời giải:

a) Nếu hai đại lượng tỉ lệ thuận với nhau thì tỉ số hai giá trị tương ứng của chúng luôn không đổi.

b) Nếu hai đại lượng tỉ lệ nghịch với nhau thì tích hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ).

2.

Phương pháp:

+) \(x, y, z\) tỉ lệ với \(a; b; c\) thì \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c}\)   

+) Tính chất của dãy tỉ số bằng nhau: \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{mx + ny + pz}}{{ma + nb + pc}}\)\(\,\,\left( {a;b;c;ma + nb + pc \ne 0} \right)\)

Lời giải:

\(x, y, z\) tỉ lệ với \(3;5;7\) nên ta có: \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{7}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{7} = \dfrac{{ - x + y}}{{ - 3 + 5}} = \dfrac{{y - x}}{{ - 3 + 5}} = \dfrac{{10}}{2} = 5\)

+) \(\dfrac{x}{3} = 5 \Rightarrow x = 3.5 = 15\)

+) \(\dfrac{y}{5} = 5 \Rightarrow y = 5.5 = 25\)

+) \(\dfrac{z}{7} = 5 \Rightarrow z = 7.5 = 35.\)

Chọn B.

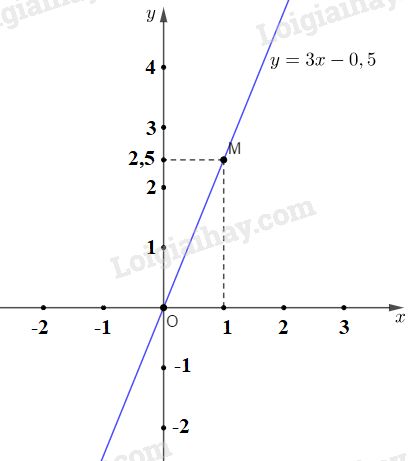
Câu 2:

Phương pháp:

+) Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một hằng số (bằng hệ số tỉ lệ).

\({x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a\)

+) Tính chất của dãy tỉ số bằng nhau:

\(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}}\)\(\,\,\left( {a;b;c;a + b + c \ne 0} \right)\)

Lời giải:

Gọi ba phần được chia lần lượt là \(x;y;z\,\,\left( {0 < x;y;z < 635} \right)\)

Theo đề bài ba phần tỉ lệ nghịch với \(4;7 \) và \(9\) nên ta có:

\(4x = 7y = 9z\)

Hay \(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{7}}} = \dfrac{z}{{\dfrac{1}{9}}}\)  và \(x + y + z = 635\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{7}}} = \dfrac{z}{{\dfrac{1}{9}}} = \dfrac{{x + y + z}}{{\dfrac{1}{4} + \dfrac{1}{7} + \dfrac{1}{9}}} = \dfrac{{635}}{{\dfrac{{127}}{{252}}}} = 1260\)

+) \(\dfrac{x}{{\dfrac{1}{4}}} = 1260 \Rightarrow x = 1260.\dfrac{1}{4} = 315\)  (thỏa mãn).

+) \(\dfrac{y}{{\dfrac{1}{7}}} = 1260 \Rightarrow y = 1260.\dfrac{1}{7} = 180\)  (thỏa mãn).

+) \(\dfrac{z}{{\dfrac{1}{9}}} = 1260 \Rightarrow z = 1260.\dfrac{1}{9} = 140\)  (thỏa mãn).

Vậy ba phần được chia ra lần lượt là: \(315;\,180;\,140.\)

Câu 3:

Phương pháp:

a) Để kiểm tra xem các điểm \(A, B, C, D\) có thuộc đồ thị hàm số hay không ta thay hoành độ của từng điểm vào công thức hàm số, sau đó tính giá trị của \(y\) đối chiếu với tung độ của điểm đó, nếu trùng nhau thì điểm đó thuộc vào đồ thị hàm số đã cho.

b) Đồ thị hàm số \( y = ax + b\left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ.

- Ta lấy \(x\ne0\) bất kỳ tìm \(y\) để tìm được tọa độ điểm thứ \(2\) gọi là điểm \(A\) mà đồ thị đó đi qua.

- Vẽ đường thẳng đi qua điểm \(O\) và \(A\) ta được đồ thị cần tìm.

Lời giải:

a) Hàm số \(y = 3x - 0,5\,\,\,\,\,(1)\)

Thay \(x = 0\) vào công thức (1) ta được: \(y = 3.0 - 0,5 =  - 0,5\)  nên \(A\left( {0; - 0,5} \right)\)  thuộc đồ thị hàm số đã cho.

Thay \(x = 1\)  vào công thức (1) ta được: \(y = 3.1 - 0,5 = 2,5\)  nên \(B\left( {1;4} \right)\) không thuộc đồ thị hàm số đã cho.

Thay \(x =  - 1\) vào công thức (1) ta được: \(y = 3.\left( { - 1} \right) - 0,5 =  - 3,5\)  nên \(C\left( { - 1; - 5} \right)\)  không thuộc đồ thị hàm số đã cho.

Thay \(x =  - 0,5\)  vào công thức (1) ta được: \(y = 3.\left( { - 0,5} \right) - 0,5 =  - 2\)  nên \(D\left( { - 0,5; - 2} \right)\) thuộc đồ thị hàm số đã cho.

b) Cho \(x = 1\)  thì \(y = 3.1 - 0,5 = 2,5\)  nên \(M\left( {1;2,5} \right)\)  thuộc đồ thị hàm số \(y = 3x - 0,5\)

Vậy đường thẳng \(OM\) là đồ thị của hàm số đã cho.

Loigiaihay.com