Đề kiểm tra 45 phút chương 2 phần Đại số 7 - Đề số 2Đề kiểm tra 45 phút chương 2: Hàm số và đồ thị đề số 2 trang 83 VBT lớp 7 tập 1 có đáp án, lời giải chi tiết kèm phương pháp giải đầy đủ tất cả các bài Quảng cáo
Đề bài Câu 1 (3 điểm) 1. (1,5 điểm) Hãy điền những từ còn thiếu trong các câu sau: a) Nếu đại lượng \(y\) … đại lượng \(x\) theo công thức \(y = kx\) (với \(k\) là hằng số khác \(0\)) thì ta nói \(y …\) với \(x…\) b) Nếu hai đại lượng tỉ lệ nghịch với nhau thì tỉ số hai giá trị … của đại lượng này bằng … hai giá trị … 2. (1,5 điểm) Nếu \(y\) tỉ lệ nghịch với \(x\) và \(y =10\) khi \(x=7\) thì khi \(x=5, y = ?\) Hãy khoanh tròn vào chữ cái trước giá trị y đúng trong các giá trị sau: \(\begin{array}{l}(A)\,\,10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,12\\(C)\,14\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,16\end{array}\) Câu 2 (3,5 điểm) Ba nhóm học sinh gồm \(39\) em và mỗi nhóm phải trồng một số cây như nhau. Nhóm thứ nhất trồng xong trong \(2\) ngày, nhóm thứ hai trong \(3\) ngày và nhóm thứ ba trong \(4\) ngày. Hỏi mỗi nhóm có bao nhiêu học sinh, biết rằng mỗi em trồng được số cây như nhau. Câu 3 (3,5 điểm) Vẽ đồ thị của hàm số \(y = f\left( x \right) = 4,5x\) . Bằng đồ thị hãy tìm: a) Các giá trị \(f\left( 1 \right);f\left( { - 1} \right);f\left( { - 2} \right);f\left( 2 \right).\) b) Giá trị của x khi \(y = - 1;y = 0;y = 1;y = 4,5.\) c) Giá trị của \(x\) khi \(y\) dương, khi \(y\) âm. Lời giải chi tiết 1. Phương pháp: Sử dụng lí thuyết đại lượng tỉ lệ thuận. Sử dụng lí thuyết đại lượng tỉ lệ nghịch. Lời giải: a) Nếu đại lượng \(y\) liên hệ với đại lượng \(x\) theo công thức \(y = kx\) (với \(k\) là hằng số khác \(0\)) thì ta nói \(y\) tỉ lệ thuận với \(x\) theo hệ số tỉ lệ \(k.\) b) Nếu hai đại lượng tỉ lệ nghịch với nhau thì tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia. 2. Phương pháp: Giả sử \(x\) và \(y\) liên hệ với nhau theo công thức \(y = \dfrac{a}{x}\). - Thay \(y = 10\) và \(x = 7\) vào công thức để tìm \(a\) - Từ đó ta tìm được công thức liên hệ giữa \(x\) và \(y.\) Thay \(x=5\) vào công thức vừa tìm được để tính giá trị của \(y.\) Lời giải: Giả sử \(y\) tỉ lệ nghịch với \(x\) theo công thức \(y = \dfrac{a}{x}\,\,\left( {a \ne 0} \right)\,\,\,\,\,\,(1)\) Thay \(y = 10\) và \(x = 7\) vào (1) ta được: \(a = 10.7 = 70\) Vậy công thức liên hệ giữa \(x\) và \(y\) là \(y = \dfrac{{70}}{x}\,\,\,\,\,\,\,\,\,\,\,(2)\) Thay \(x = 5\) vào (2) ta được: \(y = \dfrac{{70}}{5} = 14\) Chọn C. Câu 2: Phương pháp: +) Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một hằng số (bằng hệ số tỉ lệ). \({x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a\) +) Tính chất của dãy tỉ số bằng nhau: \(\dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{{x + y + z}}{{a + b + c}}\)\(\,\,\left( {a;b;c;a + b + c \ne 0} \right)\) Lời giải: Gọi số học sinh nhóm thứ nhất, thứ hai, thứ ba lần lượt là \(x;y;z\,\,\,\left( {x;y;z \in {N^*};x;y;z < 39} \right)\) Vì mỗi nhóm phải trồng số cây như nhau nên số học sinh mỗi nhóm và số ngày để hoàn thành công việc là hai đại lượng tỉ lệ nghịch. Theo đề bài nhóm thứ nhất trồng xong trong \(2\) ngày, nhóm thứ hai trong \(3\) ngày và nhóm thứ ba trong \(4\) ngày nên ta có: \(2x = 3y = 4z\) hay \(\dfrac{x}{{\dfrac{1}{2}}} = \dfrac{y}{{\dfrac{1}{3}}} = \dfrac{z}{{\dfrac{1}{4}}}\) Tổng số học sinh ba nhóm là \(39\) em nên ta có: \(x + y + z = 39\) Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\dfrac{x}{{\dfrac{1}{2}}} = \dfrac{y}{{\dfrac{1}{3}}} = \dfrac{z}{{\dfrac{1}{4}}} = \dfrac{{x + y + z}}{{\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4}}} = \dfrac{{39}}{{\dfrac{{13}}{{12}}}} = 36\) +) \(\dfrac{x}{{\dfrac{1}{2}}} = 36 \Rightarrow x = 36.\dfrac{1}{2} = 18\) (thỏa mãn). +) \(\dfrac{y}{{\dfrac{1}{3}}} = 36 \Rightarrow y = 36.\dfrac{1}{3} = 12\) (thỏa mãn). +) \(\dfrac{z}{{\dfrac{1}{4}}} = 36 \Rightarrow z = 36.\dfrac{1}{4} = 9\) (thỏa mãn). Vậy số học sinh nhóm thứ nhất, thứ hai, thứ ba lần lượt là \(18;\,12;\,\,9\) em. Câu 3: Phương pháp: Đồ thị hàm số \( y = ax + b\left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ. - Ta lấy \(x\ne0\) bất kỳ tìm \(y\) để tìm được tọa độ điểm thứ \(2\) gọi là điểm \(A\) mà đồ thị đó đi qua. - Vẽ đường thẳng đi qua điểm \(O\) và \(A\) ta được đồ thị cần tìm. a) Tìm \(f(a)\), từ hoành độ \(x=a\) ta vẽ đường vuông góc với \(Ox\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó vẽ đường vuông góc với \(Oy\), giao điểm với \(Oy\) là giá trị của \(y=f(a)\). b) Với \(y=m\), từ tung độ \(y=m\) ta vẽ đường vuông góc với \(Oy\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó ta vẽ đường vuông góc với \(Ox\), giao điểm với \(Ox\) là giá trị \(x=x_o\) thỏa mãn \(y = f\left( {{x_o}} \right) = m\). c) Quan sát đồ thị trên miền \(y\) dương và \(y\) âm để đưa ra nhận xét. Lời giải: Hàm số \(y = f\left( x \right) = 4,5x\) Cho \(x = 1\) thì \(y = 4,5.1 = 4,5\) nên \(A\left( {1;4,5} \right)\) thuộc đồ thị hàm số \(y = 4,5x\) Vậy đường thẳng \(OA\) là đồ thị của hàm số đã cho.
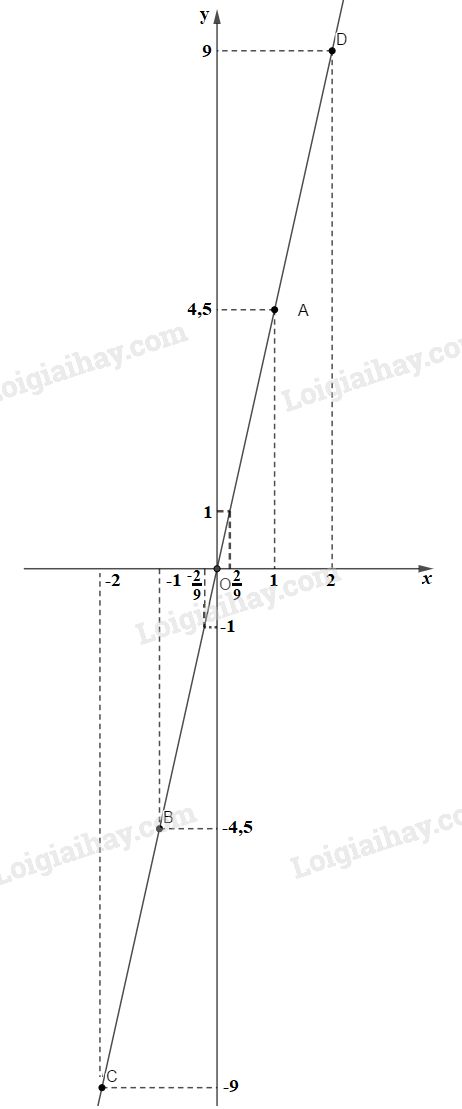
a) Tìm \(f(1)\), từ hoành độ \(x=1\) ta vẽ đường vuông góc với \(Ox\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó vẽ đường vuông góc với \(Oy\), giao điểm với \(Oy\) là giá trị của \(y=f(1)=4,5\). Bằng cách đó ta xác định được các giá trị còn lại của \(y\): \(f\left( { - 1} \right) = - 4,5;\,f\left( { - 2} \right) = - 9;\,f\left( 2 \right) = 9.\) b) Với \(y=-1\), từ tung độ \(y=-1\) ta vẽ đường vuông góc với \(Oy\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó ta vẽ đường vuông góc với \(Ox\), giao điểm với \(Ox\) là giá trị \(x = - \dfrac{2}{9}\). Bằng cách đó ta xác định được các giá trị còn lại của \(x\): Khi \(y=0\) thì \(x=0\) Khi \(y=1\) thì \(x = \dfrac{2}{9}\) Khi \(y = 4,5\) thì \(x=1.\) c) Các giá trị của \(x\) khi \(y\) dương, khi \(y\) âm. Từ đồ thị đã cho ta thấy khi \(y\) dương đồ thị nằm ở góc phần tư thứ \(I\), các điểm thuộc đồ thị có hoành độ dương (lớn hơn không). Vậy khi \(y\) dương thì \(x\) có giá trị dương. Tương tự khi \(y\) âm thì đồ thị nằm ở góc phần tư thứ \(III\), các điểm thuộc đồ thị có hoành độ âm. Vậy khi \(y\) âm thì \(x\) có giá trị âm. Loigiaihay.com
|




















Danh sách bình luận