Giải câu hỏi trắc nghiệm trang 5, 6 vở thực hành Toán 9

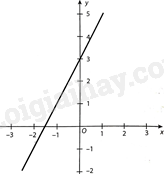
Câu 1

Trả lời Câu 1 trang 5 Vở thực hành Toán 9

Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. \({x^2} - y = 2\).

B. \(2x + y = 0\).

C. \(0x - 0y =  - 2\).

D. \({x^2} + {y^2} = 5\).

Phương pháp giải:

Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b, c, là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).

Lời giải chi tiết:

Phương trình \(2x + y = 0\) là phương trình bậc nhất hai ẩn.

Chọn B

Câu 2

Trả lời Câu 2 trang 6 Vở thực hành Toán 9

Nghiệm (tổng quát) của phương trình \( - 2x - 3y = 6\) là

A. \(\left( {x;\frac{2}{3}x + 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

B. \(\left( {\frac{3}{2}y + 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

C. \(\left( {\frac{3}{2}y - 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

D. \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Phương pháp giải:

Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.

Lời giải chi tiết:

Ta có: \( - 2x - 3y = 6\), suy ra \(y = \frac{{ - 2}}{3}x - 2\).

Do đó, nghiệm tổng quát của phương trình \( - 2x - 3y = 6\) là \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Chọn D

Câu 3

Trả lời Câu 3 trang 6 Vở thực hành Toán 9

Cho hai phương trình \( - 3x + y =  - 7\;\left( 1 \right)\) và \(x - 2y = 4\;\left( 2 \right)\). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?

A. \(\left( {0; - 7} \right)\).

B. \(\left( {6;1} \right)\).

C. \(\left( {2; - 1} \right)\).

D. \(\left( { - 1; - 10} \right)\).

Phương pháp giải:

Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lời giải chi tiết:

Với \(x = 2;y =  - 1\) ta có:

\( - 3.2 + \left( { - 1} \right) =  - 7\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (1).

\(2 - 2\left( { - 1} \right) = 4\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (2).

Do đó, \(\left( {2; - 1} \right)\) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).

Chọn C

Câu 4

Trả lời Câu 4 trang 6 Vở thực hành Toán 9

Hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn nào sau đây? trong đầu bài nó ghi là pt 1 ẩn, nhưng đúng là pt hai ẩn nên t sửa đề cho đúng luôn nhé

A. \(2x - y =  - 3\).

B. \(2x + y = 3\).

C. \(3x + y = 3\).

D. \(3x - y = 0\).

Phương pháp giải:

Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn \(ax + by = c\) là một đường thẳng. Đường thẳng đó gọi là đường thẳng \(ax + by = c\).

Lời giải chi tiết:

Ta thấy, các điểm (0; 3) và \(\left( {\frac{{ - 3}}{2};0} \right)\) thuộc đường thẳng cần tìm.

Do đó, đường thẳng cần tìm là: \(2x - y =  - 3\).

Vậy hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn \(2x - y =  - 3\).

Chọn A