Giải câu hỏi trắc nghiệm trang 18, 19 sách bài tập toán 9 - Kết nối tri thức tập 2

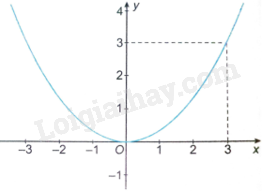
Câu 1

Trả lời câu hỏi Câu 1 trang 18 SBT Toán 9 Kết nối tri thức

Hình vẽ dưới đây là đồ thị của hàm số nào?

A. \(y = {x^2}\).

B. \(y =  - \frac{1}{2}{x^2}\).

C. \(y = \frac{1}{4}{x^2}\).

D. \(y = \frac{1}{3}{x^2}\).

Phương pháp giải:

Nhận thấy điểm (3; 3) vừa thuộc đồ thị hàm số trong hình vẽ, vừa thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên đồ thị hàm số trong hình vẽ là \(y = \frac{1}{3}{x^2}\).

Lời giải chi tiết:

Đồ thị hàm trong hình vẽ đi qua điểm (3; 3). Trong các hàm số trên, điểm (3; 3) chỉ thuộc hàm số \(y = \frac{1}{3}{x^2}\) nên hình vẽ là đồ thị của hàm số \(y = \frac{1}{3}{x^2}\).

Chọn D

Câu 2

Trả lời câu hỏi Câu 2 trang 18 SBT Toán 9 Kết nối tri thức

Cho hàm số \(y =  - \frac{2}{5}{x^2}\) có đồ thị là parabol (P). Điểm trên (P) khác gốc tọa độ O (0; 0) có tung độ gấp ba lần hoành độ thì có hoành độ là

A. \( - \frac{{15}}{2}\).

B. \(\frac{{15}}{2}\).

C. \(\frac{2}{{15}}\).

D. \( - \frac{2}{{15}}\).

Phương pháp giải:

+ Gọi tọa độ của điểm cần tìm là B(x; 3x) (với \(x \ne 0\)).

+ Vì B thuộc parabol (P) nên ta có: \(3x =  - \frac{2}{5}{x^2}\).

+ Giải phương trình thu được tìm được x.

Lời giải chi tiết:

Gọi tọa độ của điểm cần tìm là B (x; 3x) (với \(x \ne 0\)). Vì B thuộc parabol (P) nên ta có: \(3x =  - \frac{2}{5}{x^2}\)

\(\frac{2}{5}{x^2} + 3x = 0\)

\(x\left( {\frac{2}{5}x + 3} \right) = 0\)

\(x = 0\) (loại) hoặc \(\frac{2}{5}x + 3 = 0\)

\(x = \frac{{ - 15}}{2}\)

Vậy điểm thỏa mãn yêu cầu bài toán có hoành độ là \( - \frac{{15}}{2}\).

Chọn A

Câu 3

Trả lời câu hỏi Câu 3 trang 18 SBT Toán 9 Kết nối tri thức

Trong các điểm A(1; -2), B(-1; -1), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\), có bao nhiêu điểm thuộc đồ thị của hàm số \(y =  - 2{x^2}\)?

A. 2.

B. 1.

C. 3.

D. 4.

Phương pháp giải:

Thay tọa độ từng điểm vào hàm số \(y =  - 2{x^2}\), nếu đẳng thức thu được đúng thì điểm đó thuộc đồ thị hàm số.

Lời giải chi tiết:

Thay \(x = 1;y =  - 2\) vào \(y =  - 2{x^2}\) ta có: \( - 2 =  - {2.1^2}\) (luôn đúng) nên điểm A(1; -2) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

Thay \(x =  - 1;y =  - 1\) vào \(y =  - 2{x^2}\) ta có: \( - 1 =  - 2.{\left( { - 1} \right)^2}\) (vô lí) nên điểm B(-1; -1) không thuộc đồ thị hàm số \(y =  - 2{x^2}\).

Thay \(x = 10;y =  - 200\) vào \(y =  - 2{x^2}\) ta có: \( - 200 =  - {2.10^2}\) (luôn đúng) nên điểm C(10; -200) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

Thay \(x = \sqrt {10} ;y =  - 20\) vào \(y =  - 2{x^2}\) ta có: \( - 20 =  - 2.{\left( {\sqrt {10} } \right)^2}\) (luôn đúng) nên điểm \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

Vậy ba điểm A(1; -2), C(10; -200), \(D\left( {\sqrt {10} ; - 20} \right)\) thuộc đồ thị hàm số \(y =  - 2{x^2}\).

Chọn C

Câu 4

Trả lời câu hỏi Câu 4 trang 19 SBT Toán 9 Kết nối tri thức

Tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là

A. \(\left( {1;\frac{1}{2}} \right)\).

B. \(\left( {\frac{1}{2};2} \right)\).

C. \(\left( { - \frac{1}{2};1} \right)\).

D. \(\left( { - 1;\frac{1}{2}} \right)\).

Phương pháp giải:

+ Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\).

+ Giải phương trình thu được tìm được x.

+ Thay x tìm được vào \(y = x + \frac{3}{2}\), từ đó tìm được tọa độ giao điểm của d và (P).

Lời giải chi tiết:

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình: \(\frac{1}{2}{x^2} = x + \frac{3}{2}\), suy ra \({x^2} - 2x - 3 = 0\).

Vì \(1 + 2 - 3 = 0\) nên phương trình \({x^2} - 2x - 3 = 0\) có hai nghiệm \({x_1} =  - 1;{x_2} = \frac{3}{1} = 3\).

Với \(x =  - 1\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y =  - 1 + \frac{3}{2} = \frac{1}{2}\).

Với \(x = 3\) thay vào \(y = x + \frac{3}{2}\) ta có: \(y = 3 + \frac{3}{2} = \frac{9}{2}\).

Do đó, tọa độ một giao điểm của parabol (P): \(y = \frac{1}{2}{x^2}\) và đường thẳng (d): \(y = x + \frac{3}{2}\) là \(\left( { - 1;\frac{1}{2}} \right)\).

Chọn D

Câu 5

Trả lời câu hỏi Câu 5 trang 19 SBT Toán 9 Kết nối tri thức

Để điểm \(A\left( { - \frac{{\sqrt 2 }}{{\sqrt 5 }};m\sqrt 5 } \right)\) nằm trên parabol \(y =  - \sqrt 5 {x^2}\) thì giá trị của m bằng

A. \(m =  - \frac{5}{2}\).

B. \(m = \frac{2}{5}\).

C. \(m =  - \frac{2}{5}\).

D. \(m = \frac{5}{2}\).

Phương pháp giải:

Thay \(x =  - \frac{{\sqrt 2 }}{{\sqrt 5 }};y = m\sqrt 5 \) vào \(y =  - \sqrt 5 {x^2}\), thu được phương trình ẩn m, giải phương trình đó để tìm m.

Lời giải chi tiết:

Để điểm A nằm trên parabol thì: \(m\sqrt 5  =  - \sqrt 5 .{\left( {\frac{{ - \sqrt 2 }}{{\sqrt 5 }}} \right)^2} = \frac{{ - 2}}{{\sqrt 5 }}\), suy ra \(m = \frac{{ - 2}}{{\sqrt 5 }}:\sqrt 5  = \frac{{ - 2}}{5}\).

Chọn C

Câu 6

Trả lời câu hỏi Câu 6 trang 19 SBT Toán 9 Kết nối tri thức

Cho parabol (P): \(y = \left( {m - \frac{3}{4}} \right){x^2}\), với \(m \ne \frac{3}{4}\) và đường thẳng \(y = 3x - 5\). Biết đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\). Tìm m và hoành độ giao điểm còn lại của d và (P).

A. \(m = 0;x = 2\).

B. \(m = 1;x = 2\).

C. \(m = 1;x = 10\).

D. \(m = \frac{5}{4};x = 10\).

Phương pháp giải:

+ Gọi D là giao điểm của d và (P).

+ Vì d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), từ đó tìm được x và tìm được tọa độ của D.

+ Thay tọa độ điểm D vào \(y = \left( {m - \frac{3}{4}} \right){x^2}\), thu được phương trình ẩn m, giải phương trình tìm được m.

Lời giải chi tiết:

Gọi D là giao điểm của d và (P). Vì đường thẳng d cắt (P) tại một điểm có tung độ \(y = 1\) nên ta có: \(1 = 3.x - 5\), suy ra \(x = 2\). Do đó, D(2; 1).

Vì D(2; 1) thuộc (P) nên ta có: \(1 = \left( {m - \frac{3}{4}} \right){.2^2}\), suy ra \(4m - 3 = 1\), suy ra \(m = 1\).

Chọn B

Câu 7

Trả lời câu hỏi Câu 7 trang 19 SBT Toán 9 Kết nối tri thức

Không giải phương trình, hãy tính tổng hai nghiệm của phương trình \( - 3{x^2} + 5x + 1 = 0\).

A. \( - \frac{5}{6}\).

B. \(\frac{5}{3}\).

C. \( - \frac{5}{3}\).

D. \(\frac{5}{6}\).

Phương pháp giải:

Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\).  Nếu \(\Delta  > 0\) thì áp dụng định lí Viète để tính tổng các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a}\).

Lời giải chi tiết:

Vì \(\Delta  = {5^2} - 4.\left( { - 3} \right).1 = 37 > 0\) nên phương trình có hai nghiệm. Theo định lí Viète ta có tổng hai nghiệm của phương trình là: \(\frac{{ - 5}}{{ - 3}} = \frac{5}{3}\)

Chọn B

Câu 8

Trả lời câu hỏi Câu 8 trang 19 SBT Toán 9 Kết nối tri thức

Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \( - {x^2} - 4x + 6 = 0\). Không giải phương trình, tính giá trị của biểu thức \(M = \frac{1}{{{x_1} + 2}} + \frac{1}{{{x_2} + 2}}\).

A. \(M = 0\).

B. \(M = 1\).

C. \(M = 4\).

D. \(M =  - 2\).

Phương pháp giải:

+ Viết định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2};{x_1}.{x_2}\).

+ Biến đổi \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\), với \({x_1} + {x_2};{x_1}.{x_2}\) đã tính ở trên, ta tính M.

Lời giải chi tiết:

Ta có: \(M = \frac{{{x_2} + 2 + {x_1} + 2}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}} = \frac{{\left( {{x_1} + {x_2}} \right) + 4}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\)

Theo định lí Viète ta có: \({x_1} + {x_2} = \frac{{ - \left( { - 4} \right)}}{{ - 1}} =  - 4;{x_1}.{x_2} = \frac{6}{{ - 1}} =  - 6\). Do đó, \(M = \frac{{ - 4 + 4}}{{ - 6 + 2.\left( { - 4} \right) + 4}} = 0\).

Chọn A

Câu 9

Trả lời câu hỏi Câu 9 trang 19 SBT Toán 9 Kết nối tri thức

Tìm điều kiện của tham số m để phương trình \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 3m + 5 = 0\) có hai nghiệm phân biệt.

A. \(m \le  - 1\).

B. \(m =  - 1\).

C. \(m >  - 1\).

D. \(m <  - 1\).

Phương pháp giải:

Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt.

Lời giải chi tiết:

Phương trình đã cho có hai nghiệm phân biệt khi \(\Delta ' > 0\) nên \({\left[ { - \left( {m - 2} \right)} \right]^2} - 1.\left( {{m^2} - 3m + 5} \right) > 0\)

\({m^2} - 4m + 4 - {m^2} + 3m - 5 > 0\)

\( - m - 1 > 0\)

\(m <  - 1\)

Chọn D

Câu 10

Trả lời câu hỏi Câu 10 trang 19 SBT Toán 9 Kết nối tri thức

Nếu hai số u, v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình nào?

A. \({x^2} + 7x - 8 = 0\).

B. \({x^2} - 7x - 8 = 0\).

C. \({x^2} + 7x + 8 = 0\).

D. \({x^2} - 7x + 8 = 0\).

Phương pháp giải:

Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).

Lời giải chi tiết:

Nếu hai số u và v có tổng là 7 và tích là -8 thì chúng là hai nghiệm của phương trình \({x^2} - 7x - 8 = 0\)

Chọn B