Giải bài 6.33 trang 20 sách bài tập toán 9 - Kết nối tri thức tập 2Cho hai hàm số: (y = - frac{3}{2}{x^2}) và (y = {x^2}). a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ. b) Tìm điểm A nằm trên đồ thị của hàm số (y = - frac{3}{2}{x^2}) và điểm B nằm trên đồ thị của hàm số (y = {x^2}), biết rằng chúng đều có hoành độ (x = frac{3}{2}). c) Gọi A’, B’ lần lượt là các điểm đối xứng của A, B qua trục tung Oy. Tìm tọa độ của A’, B’ và chứng minh hai điểm này tương ứng nằm trên hai đồ thị của hàm số đi qua A, B. Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Quảng cáo
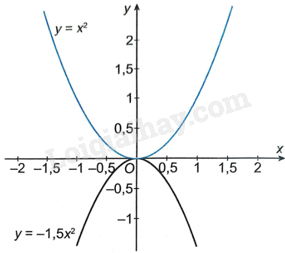
Đề bài Cho hai hàm số: \(y = - \frac{3}{2}{x^2}\) và \(y = {x^2}\). a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ. b) Tìm điểm A nằm trên đồ thị của hàm số \(y = - \frac{3}{2}{x^2}\) và điểm B nằm trên đồ thị của hàm số \(y = {x^2}\), biết rằng chúng đều có hoành độ \(x = \frac{3}{2}\). c) Gọi A’, B’ lần lượt là các điểm đối xứng của A, B qua trục tung Oy. Tìm tọa độ của A’, B’ và chứng minh hai điểm này tương ứng nằm trên hai đồ thị của hàm số đi qua A, B. Phương pháp giải - Xem chi tiết a) Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\): + Lập bảng ghi một số cặp giá trị tương ứng của x và y. + Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\). b) + Thay \(x = \frac{3}{2}\) vào \(y = - \frac{3}{2}{x^2}\) ta tìm được y, từ đó tìm được tọa độ điểm A. + Thay \(x = \frac{3}{2}\) vào \(y = {x^2}\) ta tìm được y, từ đó tìm được tọa độ điểm B. c) + Hai điểm \(\left( { - {x_o};{y_o}} \right)\) và \(\left( {{x_o};{y_o}} \right)\) là hai điểm đối xứng với nhau qua trục Oy. + Thay tọa độ của A’, B’ vào các hàm số \(y = - \frac{3}{2}{x^2}\) và \(y = {x^2}\), ta thu được các đẳng thức luôn đúng nên hai điểm A’, B’ thuộc các đồ thị hàm số đó. Lời giải chi tiết a) + Vẽ đồ thị hàm số \(y = - \frac{3}{2}{x^2}\): Lập bảng một số giá trị tương ứng giữa x và y.
Biểu diễn các điểm \(\left( { - 2; - 6} \right);\left( { - 1; - \frac{3}{2}} \right);\left( {0;0} \right);\left( {1; - \frac{3}{2}} \right),\left( {2; - 6} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = - \frac{3}{2}{x^2}\). + Vẽ đồ thị hàm số \(y = {x^2}\): Lập bảng một số cặp giá trị tương ứng giữa x và y. Biểu diễn các điểm \(\left( { - 2;4} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1;1} \right);\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = {x^2}\). b) Thay \(x = \frac{3}{2}\) vào \(y = - \frac{3}{2}{x^2}\) ta có \(y = - \frac{3}{2}.{\left( {\frac{3}{2}} \right)^2} = \frac{{ - 27}}{8}\) nên \(A\left( {\frac{3}{2};\frac{{ - 27}}{8}} \right)\). Thay \(x = \frac{3}{2}\) vào \(y = {x^2}\) ta có: \(y = {\left( {\frac{3}{2}} \right)^2} = \frac{9}{4}\) nên \(B\left( {\frac{3}{2};\frac{9}{4}} \right)\). c) Vì A’ đối xứng với \(A\left( {\frac{3}{2};\frac{{ - 27}}{8}} \right)\) qua trục tung Oy nên \(A'\left( {\frac{{ - 3}}{2};\frac{{ - 27}}{8}} \right)\). Vì B’ đối xứng với \(B\left( {\frac{3}{2};\frac{9}{4}} \right)\) qua trục tung Oy nên \(B'\left( {\frac{{ - 3}}{2};\frac{9}{4}} \right)\). Thay \(x = \frac{{ - 3}}{2};y = \frac{{ - 27}}{8}\) vào \(y = - \frac{3}{2}{x^2}\) ta có: \(\frac{{ - 27}}{8} = - \frac{3}{2}.{\left( { - \frac{3}{2}} \right)^2}\) (luôn đúng) nên A’ thuộc đồ thị của hàm số \(y = - \frac{3}{2}{x^2}\). Thay \(x = \frac{{ - 3}}{2};y = \frac{9}{4}\) vào \(y = {x^2}\) ta có: \(\frac{9}{4} = {\left( {\frac{{ - 3}}{2}} \right)^2}\) (luôn đúng) nên B’ thuộc đồ thị của hàm số \(y = {x^2}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
