Bài tập trắc nghiệm trang 137, 138, 139 SBT hình học 12Giải bài tập trắc nghiệm trang 137, 138, 139 sách bài tập hình học 12 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Chọn đáp án đúng: 3.77 Phương trình chính tắc của đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là:
Lời giải chi tiết: Ta có: \(\overrightarrow {AB} = \left( {2; - 3;4} \right)\) Đường thẳng AB đi qua điểm A(1; 2; -3) và có vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2; - 3;4} \right)\) nên có phương trình chính tắc là: \(\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{{ - 3}} = \dfrac{{z + 3}}{4}\) Chọn C. 3.78 Tọa độ giao điểm M của đường thẳng \(d:\dfrac{{x - 12}}{4} = \dfrac{{y - 9}}{3} = \dfrac{{z - 1}}{1}\) và mặt phẳng (α): 3x + 5y - z - 2 = 0 là: A. (1; 0; 1) B. (0; 0; -2) C. (1; 1; 6) D. (12; 9; 1) Lời giải chi tiết: Gọi M(12 + 4t; 9 + 3t; 1 + t) thuộc d và mặt phẳng (α), Thay tọa độ M vào phương trình (α) ta được phương trình theo t: 3(12 + 4t) + 5(9 + 3t) - (1 + t) - 2 = 0 \( \Leftrightarrow 36 + 12t + 45 + 15t - 1 - t - 2 = 0\) \( \Leftrightarrow 26t + 78 = 0 \Leftrightarrow t = - 3\) Vậy d cắt (α) tại M(0; 0; -2). Chọn B. 3.79 Cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 + 2t\end{array} \right.\) và mặt phẳng (α): x + 3y + z + 1 = 0 Khẳng định nào sau đây là đúng? A. d // (α) B. d cắt (α) C. d ⊂ (α) D. d ⊥ (α) Lời giải chi tiết: Đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 1;2} \right)\) Mặt phẳng (α) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;3;1} \right)\) Ta thấy: \(\overrightarrow u .\overrightarrow n = 1.1 - 1.3 + 2.1 = 0\) nên \(\overrightarrow u \bot \overrightarrow n \) Mà điểm cố định M(1; 2; 1) của d không thuộc (α). Vậy d // (α) Chọn A. 3.80 Cho đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{{y - 1}}{2} = \dfrac{{z - 2}}{{ - 3}}\) và mặt phẳng (α): x + y + z - 4 = 0 Khẳng định nào sau đây là đúng? A. d cắt (α) B. d // (α) C. d ⊂ (α) D. d ⊥ (α) Lời giải chi tiết: Đường thẳng d có vectơ chỉ phương là \(\overrightarrow u = \left( {1;2; - 3} \right)\) Mặt phẳng (α) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;1;1} \right)\) Ta thấy: \(\overrightarrow u .\overrightarrow n = 1.1 + 2.1 - 3.1 = 0\) nên \(\overrightarrow u \bot \overrightarrow n \) Mà điểm cố định M(1; 1; 2) của d nằm trên (α). Vậy d ⊂ (α) Chọn C. 3.81 Hãy tìm kết luận đúng về vị trí tương đối giữa hai đường thẳng:
A. d cắt d' B. d ≡ d' C. d chéo với d' D. d // d' Lời giải chi tiết: Ta thấy: \(d\) có VTCP \(\overrightarrow {{u_1}} = \left( {1;1; - 1} \right)\) và đi qua \(M\left( {1;2;3} \right)\) \(d'\) có VTCP \(\overrightarrow {{u_2}} = \left( {2;2; - 2} \right)\). Có \(\overrightarrow {{u_2}} = 2\overrightarrow {{u_1}} \) và thay tọa độ của M vào \(d'\) ta được: \(\left\{ \begin{array}{l}1 = 1 + 2t'\\2 = - 1 + 2t'\\3 = 3 - 2t'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t' = 0\\t' = \dfrac{3}{2}\\t' = 0\end{array} \right.\left( {vo\,li} \right)\) nên \(M \notin d'\) Hai đường thẳng d và d' có hai vectơ chỉ phương tỉ lệ và một điểm của đường này không nằm trên đường kia. Suy ra d // d'. Chọn D. 3.82 Giao điểm giữa hai đường thẳng:
A. (-3; -2; 6) B. (5; -1; 20) C. (3; 7; 18) D. (3; -2; 1) Lời giải chi tiết: Giải hệ phương trình: \(\left\{ \begin{array}{l} - 3 + 2t = 5 + t'\\ - 2 + 3t = - 1 - 4t'\\6 + 4t = 20 + t'\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2t - t' = 8\\3t + 4t' = 1\\4t - t' = 14\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}t = 3\\t' = - 2\end{array} \right.\) Vậy giao điểm của d và d' là M(3; 7; 18). Chọn C. 3.83 Tìm m để hai đường thẳng sau đây cắt nhau:
A. m = 0 B. m = 1 C. m = -1 D. m = 2 Lời giải chi tiết: \(d\) có VTCP \(\overrightarrow u = \left( {m;1;2} \right)\) và đi qua M(1; 0; -1) \(d'\) có VTCP \(\overrightarrow {u'} = \left( { - 1;2; - 1} \right)\) và đi qua M'(1; 2; 3) Ta có: \(\overrightarrow {MM'} = \left( {0;2;4} \right)\), \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \left( { - 2;m - 2;2m + 1} \right)\) d và d' cắt nhau ⇔ \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MM'} = 0\) ⇔ 2(m - 2) + 4(2m + 1) = 0 ⇔ m = 0 Chọn A. 3.84 Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (α): 2x - y + 2z - 3 = 0 là: A. 3 B. 2 C. 1 D. 11 Lời giải chi tiết: Ta có: \(d\left( {M,\left( \alpha \right)} \right)\) \( = \dfrac{{\left| {2.\left( { - 2} \right) - \left( { - 4} \right) + 2.3 - 3} \right|}}{{\left| {{2^2} + {1^2} + {2^2}} \right|}}\) \( = \dfrac{3}{3} = 1\) Chọn C. 3.85 Gọi H là hình chiếu vuông góc của điểm A(2; -1; -1) đến mặt phẳng (α): 16x - 12y - 15z - 4 = 0. Độ dài của đoạn AH là: A. 55 B. 11/5 C. 11/25 D. 22/5 Lời giải chi tiết: Ta có: \(AH = d\left( {A,\left( \alpha \right)} \right)\)\( = \dfrac{{\left| {16.2 - 12.\left( { - 1} \right) - 15.\left( { - 1} \right) - 4} \right|}}{{\sqrt {{{16}^2} + {{12}^2} + {{15}^2}} }}\) \( = \dfrac{{55}}{{25}} = \dfrac{{11}}{5}\) Chọn B. 3.86 Cho mặt cầu tâm I(4; 2; -2) bán kính r tiếp xúc với mặt phẳng (P): 12x - 5z - 19 = 0. Bán kính r bằng: A. 39 B. 3 C. 13 D. 39/√(13) Lời giải chi tiết: Mặt cầu tâm I bán kính r tiếp xúc với mặt phẳng (P) khi \(R = d\left( {I,\left( P \right)} \right)\)\( = \dfrac{{\left| {12.4 - 5.\left( { - 2} \right) - 19} \right|}}{{\sqrt {{{12}^2} + {5^2}} }}\) \( = \dfrac{{39}}{{13}} = 3\) Chọn B. 3.87 Cho hai mặt phẳng song song: (α): x + y - z + 5 = 0 và (β): 2x + 2y - 2z + 3 = 0 Khoảng cách giữa (α) và (β) là: A. 2/(√3) B. 2 C. 7/2 D. 7/(2√3) Lời giải chi tiết: Lấy điểm M(0; 0; 5) thuộc (α). Do \(\left( \alpha \right)//\left( \beta \right)\) nên \(d\left( {\left( \alpha \right),\left( \beta \right)} \right) = d\left( {M,\left( \beta \right)} \right)\) \( = \dfrac{{\left| {2.0 + 2.0 - 2.5 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + {2^2}} }} = \dfrac{7}{{2\sqrt 3 }}\) Chọn D. 3.88 Khoảng cách từ điểm M(2; 0; 1) đến đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) là: A. √(12) B. √3 C. √2 D. 12/(√6) Lời giải chi tiết: Lấy điểm A(1; 0; 2) trên d và một vectơ chỉ phương của d là \(\overrightarrow u = \left( {1;2;1} \right)\) \(\overrightarrow {AM} = \left( {1;0; - 1} \right)\) \( \Rightarrow \left[ {\overrightarrow {AM} ,\overrightarrow u } \right] = \left( {2; - 2;2} \right)\) \(d\left( {M,d} \right) = \dfrac{{\left| {\left[ {\overrightarrow {AM} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) \( = \dfrac{{\sqrt {{2^2} + {2^2} + {2^2}} }}{{\sqrt {{1^2} + {2^2} + {1^2}} }} = \sqrt 2 \) Chọn C. 3.89 Bán kính của mặt cầu tâm I(1; 3; 5) và tiếp xúc với đường thẳng \(\left\{ \begin{array}{l}x = t\\y = - 1 - t\\z = 2 - t\end{array} \right.\) là: A. √(14) B. 14 C. √7 D. 7 Lời giải chi tiết: Đường thẳng \(d\) đi qua điểm \(A\left( {0; - 1;2} \right)\) và VTCP \(\overrightarrow u = \left( {1; - 1; - 1} \right)\). \( \Rightarrow \overrightarrow {IA} = \left( { - 1; - 4; - 3} \right)\) \( \Rightarrow \left[ {\overrightarrow {IA} ,\overrightarrow u } \right] = \left( {1; - 4;5} \right)\) \( \Rightarrow R = d\left( {I,d} \right) = \dfrac{{\left| {\left[ {\overrightarrow {IA} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) \( = \dfrac{{\sqrt {1 + {4^2} + {5^2}} }}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \sqrt {14} \) Chọn A. 3.90 Khoảng cách giữa hai đường thẳng:
A. √6 B. (√6)/2 C. 1/(√6) D. √2 Lời giải chi tiết: d đi qua điểm M(1; -1; 1) và có vectơ chỉ phương \(\overrightarrow u \) = (2; -1; 0); d' đi qua điểm M'(2; -2; 3) và có vectơ chỉ phương \(\overrightarrow {u'} \) = (-1; 1; 1) Ta có: \(\overrightarrow {MM'} = \left( {1; - 1;2} \right)\), \(\left[ {\overrightarrow u ,\overrightarrow {u'} } \right] = \left( { - 1; - 2;1} \right)\) \(d\left( {d,d'} \right) = \dfrac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MM'} } \right|}}{{\left| {\left[ {\overrightarrow u ,\overrightarrow {u'} } \right]} \right|}}\) \( = \dfrac{{\left| { - 1.1 - 2.\left( { - 1} \right) + 1.2} \right|}}{{\sqrt {{1^2} + {2^2} + {1^2}} }}\) \( = \dfrac{3}{{\sqrt 6 }} = \dfrac{{\sqrt 6 }}{2}\) Ta được khoảng cách giữa hai đường thẳng d và d' bằng (√6)/2. Chọn B. 3.91 Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) A. (1; 0; 2) B. (2; 2; 3) C. (0; -2; 1) D. (-1; -4; 0) Lời giải chi tiết: Đường thẳng \(\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) có phương trình tham số là: \(\left\{ \begin{array}{l}x = 1 + t\\y = 2t\\z = 2 + t\end{array} \right.\). Gọi H(1 + t; 2t; 2 + t) là một điểm trên Δ \( \Rightarrow \overrightarrow {MH} = \left( { - 1 + t;2t;1 + t} \right)\) \(\Delta \) có VTCP \(\overrightarrow {{u_\Delta }} = \left( {1;2;1} \right)\) H là hình chiếu vuông góc của M trên Δ \( \Leftrightarrow \overrightarrow {MH} .\overrightarrow {{u_\Delta }} = 0\) \(\begin{array}{l} \Leftrightarrow 1.\left( { - 1 + t} \right) + 2.2t + 1.\left( {1 + t} \right) = 0\\ \Leftrightarrow - 1 + t + 4t + 1 + t = 0\\ \Leftrightarrow t = 0\end{array}\) Suy ra H(1; 0; 2) Chọn A. 3.92 Cho mặt phẳng (α): 3x - 2y - z + 5 = 0 và đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y - 7}}{1} = \dfrac{{z - 3}}{4}\) Gọi (β) là mặt phẳng chứa Δ và song song với (α). Khoảng cách giữa (α) và (β) là: A. 9/14 B. 9/(√(14)) C. 3/14 D. 3/(√(14)) Lời giải chi tiết: Lấy điểm \(M\left( {1;7;3} \right) \in \Delta \subset \left( \beta \right)\) Do \(\left( \beta \right)//\left( \alpha \right)\) nên \(d\left( {\left( \beta \right),\left( \alpha \right)} \right) = d\left( {M,\left( \alpha \right)} \right)\) Ta có: \(d\left( {M,\left( \alpha \right)} \right) = \dfrac{{\left| {3.1 - 2.7 - 3 + 5} \right|}}{{\sqrt {{3^2} + {2^2} + {1^2}} }}\) \( = \dfrac{9}{{\sqrt {14} }}\) Chọn B. Loigiaihay.com
|














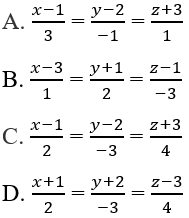
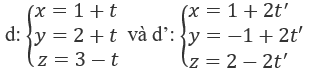
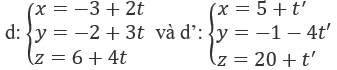
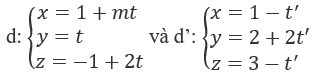
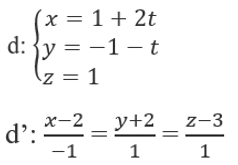






Danh sách bình luận