Giải bài tập 5.8 trang 39 SGK Toán 12 tập 2 - Kết nối tri thứcBác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không? Quảng cáo
Đề bài Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?
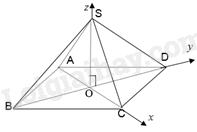
Phương pháp giải - Xem chi tiết Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\). Lời giải chi tiết Đặt tên bốn mái của ngôi nhà và chọn hệ trục tọa độ như hình sau:
Giả sử hình vuông ABCD cạnh a và các cạnh bên bằng nhau có độ dài là b. Vì ABCD là hình vuông, O là giao điểm của AC và BD nên \(OC = OD = OB = \frac{{a\sqrt 2 }}{2}\) Tam giác SOC vuông tại O nên \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \sqrt {\frac{{2{b^2} - {a^2}}}{2}} \) Khi đó, \(O\left( {0;0;0} \right),C\left( {\frac{{a\sqrt 2 }}{2};0;0} \right),D\left( {0;\frac{{a\sqrt 2 }}{2};0} \right),B\left( {0;\frac{{ - a\sqrt 2 }}{2};0} \right),S\left( {0;0;\sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right)\) \(\overrightarrow {SC} \left( {\frac{{a\sqrt 2 }}{2};0; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right),\overrightarrow {DC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{ - a\sqrt 2 }}{2};0} \right),\overrightarrow {BC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{a\sqrt 2 }}{2};0} \right)\) \(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\{ - 1}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&{ - 1}\end{array}} \right|} \right)\) \( = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\) \(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&1\end{array}} \right|} \right) = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\) Mặt phẳng (SCD) nhận \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến. Mặt phẳng (SCB) nhận \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến. Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^2}}}{2} \ne 0\) Do đó, hai mặt phẳng (SCD) và (SCB) không vuông góc với nhau. Vậy không thể thực hiện được ý tưởng trên.
|





















Danh sách bình luận