Giải bài tập 5.40 trang 85 SGK Toán 12 tập 2 - Cùng khám pháTrong các chương trình đồ hoạ máy tính, để tạo ảo giác theo đúng phối cảnh, các vật ở càng gần thì càng lớn hơn các vật ở xa, các hình ảnh ba chiều trong bộ nhớ của máy tính được chiếu lên một màn hình hình chữ nhật từ điểm nhìn của mắt hoặc máy chiếu. Quảng cáo
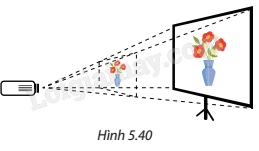
Đề bài Trong các chương trình đồ hoạ máy tính, để tạo ảo giác theo đúng phối cảnh, các vật ở càng gần thì càng lớn hơn các vật ở xa, các hình ảnh ba chiều trong bộ nhớ của máy tính được chiếu lên một màn hình hình chữ nhật từ điểm nhìn của mắt hoặc máy chiếu. Không gian quan sát, một phần của không gian được nhìn thấy là vùng nằm trong bốn mặt phẳng đi qua điểm nhìn và một đường biên của màn hình. Nếu vật trong cảnh vật mở rộng vượt quá bốn mặt phẳng này thì chúng phải được cắt xén trước khi dữ liệu điểm ảnh được gửi đến màn hình. Vì vậy các mặt phẳng này được gọi là mặt phẳng cắt. Giả sử màn hình được biểu diễn bởi hình chữ nhật trong mặt phẳng Oyz với các đỉnh (0; 400; 0), (0; −400; 0), (0; 400; 600), (0; −400; 600) và máy quay được đặt tại (1000; 0; 0). Tính góc giữa màn hình và các mặt phẳng cắt.
Phương pháp giải - Xem chi tiết - Xác định mặt phẳng chứa màn hình dựa trên các điểm đã cho. - Xác định các mặt phẳng cắt đi qua điểm máy quay và các cạnh của màn hình. - Tính góc giữa mặt phẳng chứa màn hình và từng mặt phẳng cắt bằng công thức góc giữa hai mặt phẳng: \(\cos \theta = \frac{{|{{\vec n}_{{\rm{screen}}}} \cdot {{\vec n}_{{\rm{cut}}}}|}}{{|{{\vec n}_{{\rm{screen}}}}||{{\vec n}_{{\rm{cut}}}}|}}\). Lời giải chi tiết - Các điểm \(A = (0;400;0)\), \(B = (0; - 400;0)\), \(C = (0;400;600)\), và \(D = (0; - 400;600)\) đều nằm trong mặt phẳng Oyz, do đó phương trình của mặt phẳng chứa màn hình là: \(x = 0\) - Vectơ pháp tuyến của mặt phẳng này là \(\overrightarrow {{n_1}} = (1;0;0)\). - Điểm máy quay \(O = (1000;0;0)\). * Mặt phẳng cắt qua điểm O và cạnh AB: - Vectơ \(\overrightarrow {OA} = ( - 1000;400;0)\), \(\overrightarrow {OB} = ( - 1000; - 400;0)\) - Vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng này là tích có hướng của \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \): \(\overrightarrow {{n_2}} = \overrightarrow {OA} \times \overrightarrow {OB} = (0;0;800000)\) - Đơn giản hóa, ta có \(\overrightarrow {{n_2}} = (0;0;1)\). * Mặt phẳng cắt qua điểm O và cạnh BC: - Vectơ \(\overrightarrow {OB} = ( - 1000; - 400;0)\), \(\overrightarrow {OC} = ( - 1000;400;600)\) - Vectơ pháp tuyến \(\overrightarrow {{n_3}} \) của mặt phẳng này: \(\overrightarrow {{n_3}} = \overrightarrow {OB} \times \overrightarrow {OC} = ( - 240000;600000; - 800000)\) - Đơn giản hóa, ta có \(\overrightarrow {{n_3}} = ( - 6;15; - 20)\). * Mặt phẳng cắt qua điểm O và cạnh AD: - Vectơ \(\overrightarrow {OA} = ( - 1000;400;0)\), \(\overrightarrow {OD} = ( - 1000; - 400;600)\) - Vectơ pháp tuyến \(\overrightarrow {{n_4}} \) của mặt phẳng này là tích có hướng của \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \): \(\overrightarrow {{n_4}} = \overrightarrow {OA} \times \overrightarrow {OD} = (240000;600000;800000)\) - Đơn giản hóa, ta có \(\overrightarrow {{n_4}} = (6;15;20)\). * Mặt phẳng cắt qua điểm O và cạnh DC: - Vectơ \(\overrightarrow {OD} = ( - 1000; - 400;600)\), \(\overrightarrow {OC} = ( - 1000;400;600)\) - Vectơ pháp tuyến \(\overrightarrow {{n_5}} \) của mặt phẳng này: \(\overrightarrow {{n_5}} = \overrightarrow {OB} \times \overrightarrow {OC} = ( - 480000;0; - 800000)\) - Đơn giản hóa, ta có \(\overrightarrow {{n_5}} = ( - 3;0; - 5)\). * Tính góc giữa mặt phẳng chứa màn hình và các mặt phẳng cắt: - Góc giữa mặt phẳng chứa màn hình và mặt phẳng qua cạnh AB: \(\cos {\theta _1} = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_2}} |}} = \frac{{|(1;0;0) \cdot (0;0;1)|}}{{1 \cdot 1}} = 0\) \( \Rightarrow {\theta _1} = {90^\circ }\). - Góc giữa mặt phẳng chứa màn hình và mặt phẳng qua cạnh BC: \(\cos {\theta _2} = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_3}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_3}} |}} = \frac{{|(1;0;0) \cdot ( - 6;15; - 20)|}}{{1 \cdot \sqrt {{{( - 6)}^2} + {{15}^2} + {{( - 20)}^2}} }} = \frac{{ - 6}}{{\sqrt {661} }} \approx 0,2334\) \( \Rightarrow {\theta _2} \approx 103,{5^\circ }\). - Góc giữa mặt phẳng chứa màn hình và mặt phẳng qua cạnh AD: \(\cos {\theta _2} = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_4}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_4}} |}} = \frac{{|(1;0;0) \cdot (6;15;20)|}}{{1 \cdot \sqrt {{6^2} + {{15}^2} + {{20}^2}} }} = \frac{6}{{\sqrt {661} }} \approx 0,2334\) \( \Rightarrow {\theta _3} \approx 76,{5^\circ }\). - Góc giữa mặt phẳng chứa màn hình và mặt phẳng qua cạnh DC: \(\cos {\theta _2} = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_5}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_5}} |}} = \frac{{|(1;0;0) \cdot ( - 3;0; - 5)|}}{{1 \cdot \sqrt {{{( - 3)}^2} + {{( - 5)}^2}} }} = \frac{{ - 3}}{{\sqrt {34} }} \approx 0,5145\) \( \Rightarrow {\theta _5} \approx 120,{96^\circ }\).
|




















Danh sách bình luận