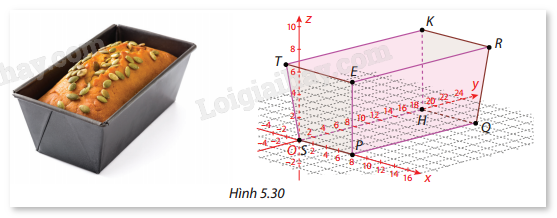
Giải bài tập 5.29 trang 71 SGK Toán 12 tập 2 - Cùng khám pháMột khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn. Quảng cáo
Đề bài Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Phương pháp giải - Xem chi tiết 1. Tính góc giữa hai cạnh kề - Xác định vectơ chỉ phương của hai cạnh: - Sử dụng công thức tính góc giữa hai vectơ: \(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\) 2. Tính góc giữa cạnh bên và mặt đáy: - Xác định các vectơ chỉ phương của cạnh bên và mặt đáy. - Sử dụng công thức tính góc giữa hai vectơ: \(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\) 3. Tính góc giữa mặt bên và mặt đáy: - Tính vectơ pháp tuyến của mặt bên và mặt đáy. - Sử dụng công thức tính góc giữa hai mặt phẳng: \(\cos \theta = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_2}} |}}\) Lời giải chi tiết - Tính góc giữa hai cạnh kề nhau: Ta có các vectơ chỉ phương sau: \(\overrightarrow {SP} = P - S = (8 - 0;0 - 0;0 - 0) = (8;0;0)\) \(\overrightarrow {SQ} = Q - S = (8 - 0;18 - 0;0 - 0) = (8;18;0)\) \(\overrightarrow {ST} = T - S = ( - 1 - 0; - 1 - 0;7 - 0) = ( - 1; - 1;7)\) \(\overrightarrow {SH} = \overrightarrow {PQ} = (0;18;0)\) \(\overrightarrow {SE} = (9; - 1;7)\) Góc giữa những cặp cạnh kề nhau: \(\begin{array}{l}\cos (\overrightarrow {SP} ,\overrightarrow {ST} ) = \frac{{8.( - 1) + 0.( - 1) + 0.( - 7)}}{{\sqrt {{8^2}} .\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {{( - 7)}^2}} }} = \frac{{ - 8}}{{8.\sqrt {51} }} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {SP} ,\overrightarrow {ST} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {PS} ,\overrightarrow {PE} ) = (\overrightarrow {HQ} ,\overrightarrow {HK} ) = (\overrightarrow {QH} ,\overrightarrow {QR} ) \approx {98^\circ }\end{array}\) \(\begin{array}{l}\cos (\overrightarrow {EP} ,\overrightarrow {ER} ) = \frac{{( - 1).(0) + (1).(2) + ( - 7).(0)}}{{\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} .\sqrt {{0^2} + {2^2} + {0^2}} }} = \frac{2}{{\sqrt {51} .2}} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {EP} ,\overrightarrow {ER} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {RE} ,\overrightarrow {RQ} ) = (\overrightarrow {TS} ,\overrightarrow {TK} ) = (\overrightarrow {KT} ,\overrightarrow {KH} ) \approx {82^\circ }\end{array}\) \(\begin{array}{l}\cos (\overrightarrow {ET} ,\overrightarrow {EP} ) = \frac{{( - 10).( - 1) + (0).(1) + (0).( - 7)}}{{\sqrt {{{( - 10)}^2} + {0^2} + {0^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} }} = \frac{{10}}{{10.\sqrt {51} }} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {ET} ,\overrightarrow {EP} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {TE} ,\overrightarrow {TS} ) = (\overrightarrow {KH} ,\overrightarrow {KR} ) = (\overrightarrow {RK} ,\overrightarrow {RQ} ) \approx {82^\circ }\end{array}\) \(\begin{array}{l}\cos (\overrightarrow {PE} ,\overrightarrow {PQ} ) = \frac{{(1).(0) + ( - 1).(18) + (7).(0)}}{{\sqrt {{1^2} + {{( - 1)}^2} + {7^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = \frac{{ - 18}}{{\sqrt {51} .18}} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {PE} ,\overrightarrow {PQ} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {QP} ,\overrightarrow {QR} ) = (ST,\overrightarrow {SH} ) = (\overrightarrow {HS} ,\overrightarrow {HK} ) \approx {98^\circ }\end{array}\) \(\cos (\overrightarrow {SP} ,\overrightarrow {SH} ) = \frac{{8.(0) + 0.(18) + 0.(0)}}{{\sqrt {{8^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {SP} ,\overrightarrow {SH} ) = {90^\circ }\) \(\cos (\overrightarrow {PS} ,\overrightarrow {PQ} ) = \frac{{( - 8).(0) + 0.(18) + 0.(0)}}{{\sqrt {{{( - 8)}^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {PS} ,\overrightarrow {PQ} ) = {90^\circ }\) Các cặp cạnh còn lại có số đo góc là 90° - Tính góc giữa cạnh bên và mặt đáy: Chọn một cạnh bên là ST. Vectơ pháp tuyến của mặt đáy SPQH là: \(\vec n = \overrightarrow {SP} \times \overrightarrow {SQ} = (0.0 - 0.18;0.8 - 8.0;8.18 - 0.8) = (0;0;144)\) \( \Rightarrow \theta = \arccos \left( {\frac{7}{{\sqrt {51} }}} \right)\) - Tính góc giữa mặt bên và mặt đáy của khuôn. Chọn mặt bên là STEP Vectơ pháp tuyến của mặt phẳng STEP là: \(\overrightarrow {{n_{STEP}}} = \overrightarrow {SP} .\overrightarrow {ST} = (0.7 - 0.( - 1);0.( - 1) - 8.7;8.( - 1) - 0.( - 1)) = (0; - 56; - 8)\) Góc giữa mặt bên STEP và mặt đáy SPQH là: \(\cos \theta = \frac{{\left| {0.0 + 0.( - 56) + 144.( - 8)} \right|}}{{\sqrt {{{144}^2}} .\sqrt {{{( - 56)}^2} + {{( - 8)}^2}} }} = \frac{{1208}}{{144.40\sqrt 2 }} = \frac{{151}}{{720\sqrt 2 }} \Rightarrow \theta \approx 81^\circ \)
|




















Danh sách bình luận