Giải bài tập 4.42 trang 39 SGK Toán 12 tập 2 - Cùng khám phá

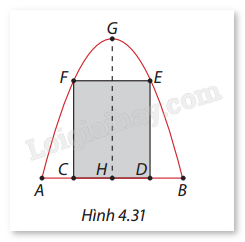
Đề bài

Một cái cổng hình parabol như Hình 4.31. Chiều cao \(GH = 4{\mkern 1mu} {\rm{m}}\), chiều rộng \(AB = 4{\mkern 1mu} {\rm{m}},AC = BD = 0,9{\mkern 1mu} {\rm{m}}\). Người ta làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm với giá 1.200.000 đồng/m², phần còn lại làm khung hoa sắt với giá 900.000 đồng/m².

A. 11 445 000 đồng.

B. 4 077 000 đồng.

C. 7 368 000 đồng.

D. 11 370 000 đồng.

Lời giải chi tiết

Phương trình của parabol có dạng:

\(y = a{x^2} + bx + c\)

Từ điểm \(G(0;4)\), ta suy ra được \(c = 4\).

\(y = a{x^2} + bx + 4\)

Theo đề bài ta có \(AB = 4m\), mà \(A,\,\,B\) là hai điểm đối xứng với nhau qua trục tung và nằm trên trục hoành nên suy ra:

\(\begin{array}{l}a{.2^2} + b.2 + 4 = 0\\a.{\left( { - 2} \right)^2} + b.\left( { - 2} \right) + 4 = 0\end{array}\)

Vậy ta có phương trình parabol là:

\(y =  - {x^2} + 4\)

Từ đề bài, ta suy ra được \(CH = DH = 1,1m\) nên độ dài của \(CF\) và \(DE\) là:

\(CF = DE =  - {(1,1)^2} + 4 = 2,79\)

Diện tích của hình chữ nhật \(CDEF\)là:

\({S_{CDEF}} = CD \times EF = 2,2 \times 2,79 = 6,138{\mkern 1mu} {{\rm{m}}^2}\)

Diện tích phần parabol là:

\({S_{{\rm{parabol}}}} = 2.\int_0^2 {( - {x^2} + 4)} {\mkern 1mu} dx = 2.\left[ { - \frac{{{x^3}}}{3} + 4x} \right]_0^2 = 2.\left( { - \frac{8}{3} + 8} \right) = \frac{{32}}{3}\)

Diện tích phần khung sắt phía trên là:

\({S_{{\rm{khung}}}} = {S_{{\rm{parabol}}}} - {S_{CDEF}} = \frac{{32}}{3} - 6,138 \approx 4,529{{\rm{m}}^2}\)

Tính tổng chi phí:

- Chi phí làm phần hình chữ nhật là:

\(6,138 \times 1\,\,200\,\,000 = 7\,\,365\,\,600\)(đồng)

- Chi phí làm phần khung sắt là:

\(4,529 \times 900.000 = 4\,\,075\,\,800\) (đồng)

Tổng chi phí làm cổng là:

\({\rm{tongcp}} = 7\,\,365\,\,600 + 4\,\,075\,\,800 = 11\,\,441\,\,400\) (đồng)

Chọn A.