Giải bài tập 2.37 trang 74 SGK Toán 12 tập 1 - Kết nối tri thứcCho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’. a) Biểu diễn \(\overrightarrow {AG} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} \) và \(\overrightarrow {AA'} \). b) Từ câu a, hãy chứng tỏ ba điểm A, G và C’ thẳng hàng. Quảng cáo
Đề bài Cho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’. Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng. Sử dụng kiến thức về trung điểm của đoạn thẳng để chứng minh: Nếu I là trung điểm của đoạn thẳng AB, với điểm M tùy ý ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \). Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) Sử dụng kiến thức về quy tắc hình hộp để chứng minh: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) b) Sử dụng kiến thức về 2 vectơ cùng phương để chứng minh ba điểm thẳng hàng: Nếu \(\overrightarrow {AB} = k\overrightarrow {AC} \) thì hai vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương và 3 điểm A, B, C thẳng hàng. Lời giải chi tiết
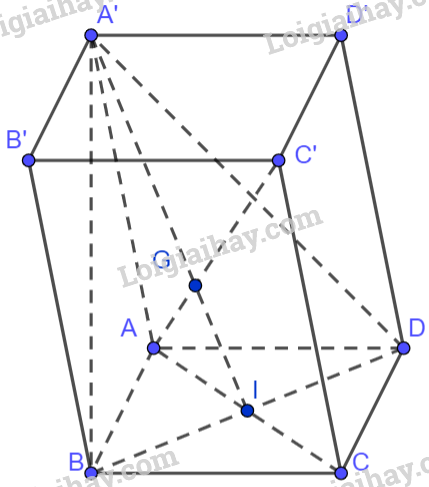
Gọi I là giao điểm của AC và BD. Vì tứ giác ABCD là hình bình hành nên I là trung điểm của BD. Do đó, A’I là đường trung tuyến của tam giác A’BD. Mà G là trọng tâm tam giác A’BD nên \(\overrightarrow {A'G} = \frac{2}{3}\overrightarrow {A'I} \). Vì I là trung điểm BD nên \(\overrightarrow {A'I} = \frac{1}{2}\left( {\overrightarrow {A'B} + \overrightarrow {A'D} } \right) = \frac{1}{2}\left( {\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} + \overrightarrow {A'A} } \right) = - \overrightarrow {AA'} + \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) Do đó, \(\overrightarrow {A'G} = - \frac{2}{3}\overrightarrow {AA'} + \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AD} \) Ta có: \(\overrightarrow {AG} = \overrightarrow {AA'} + \overrightarrow {A'G} = \overrightarrow {AA'} - \frac{2}{3}\overrightarrow {AA'} + \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AD} = \frac{1}{3}\left( {\overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} } \right)\) b) Vì ABCD.A’B’C’D’ là hình hộp nên \(\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} \) Do đó, \(\overrightarrow {AC'} = 3\overrightarrow {AG} \) nên hai vectơ \(\overrightarrow {AC'} \) và \(\overrightarrow {AG} \) cùng phương. Vậy ba điểm A, G và C’ thẳng hàng.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
