Giải bài 9.20 trang 54 sách bài tập toán 9 - Kết nối tri thức tập 2

Đề bài

Cho $\Delta ABC\backsim \Delta A'B'C'$ với tỉ số đồng dạng \(k > 0\). Gọi (O, R) và (O’, R’) lần lượt là đường tròn ngoại tiếp các tam giác ABC và A’B’C’. Gọi (I, r) và (I’, r’) lần lượt là đường tròn nội tiếp các tam giác ABC và A’B’C’. Chứng minh rằng \(\frac{R}{{R'}} = \frac{r}{{r'}} = k\).

Lời giải chi tiết

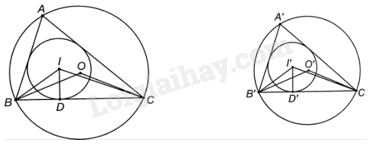
Ta có: \(\widehat {BOC} = 2\widehat {BAC}\) (góc nội tiếp và góc ở tâm của đường tròn (O) cùng chắn cung BC).

\(\widehat {B'O'C'} = 2\widehat {B'A'C'}\) (góc nội tiếp và góc ở tâm của đường tròn (O’) cùng chắn cung B’C’).

Tam giác BOC và tam giác B’O’C’ ta có:

\(\widehat {BOC} = 2\widehat {BAC} = 2\widehat {B'A'C'} = \widehat {B'O'C'}\);

\(\widehat {CBO} = \frac{{{{180}^o} - \widehat {BOC}}}{2} = \frac{{{{180}^o} - \widehat {B'O'C'}}}{2} = \widehat {C'B'O'}\)

Do đó, $\Delta BOC\backsim \Delta B'O'C'\left( g.g \right)$.

Suy ra: \(\frac{R}{{R'}} = \frac{{OB}}{{O'B'}} = \frac{{OC}}{{O'C'}} = \frac{r}{{r'}} = k\).