Giải bài 9.19 trang 54 sách bài tập toán 9 - Kết nối tri thức tập 2Cho tam giác ABC nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Tia AI cắt (O) tại X (khác A). Chứng minh rằng X là tâm của đường tròn ngoại tiếp tam giác BIC. Quảng cáo
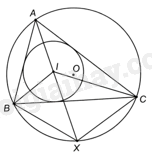
Đề bài Cho tam giác ABC nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Tia AI cắt (O) tại X (khác A). Chứng minh rằng X là tâm của đường tròn ngoại tiếp tam giác BIC. Phương pháp giải - Xem chi tiết + Chứng minh \(\widehat {BIX} = \frac{{\widehat {BAC}}}{2} + \frac{{\widehat {ABC}}}{2}\), \(\widehat {IBX} = \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {CAB}}}{2}\) nên tam giác BIX cân tại X nên \(XI = XB\). + Chứng minh tương tự ta có: \(XI = IC\). + Suy ra, X là tâm của đường tròn ngoại tiếp tam giác BIC. Lời giải chi tiết
Vì I là giao điểm của các đường phân giác của tam giác ABC nên \(\widehat {IAB} = \frac{{\widehat {BAC}}}{2};\widehat {IBA} = \widehat {IBC} = \frac{{\widehat {ABC}}}{2}\). Ta có: \(\widehat {BIX} = {180^o} - \widehat {BIA} = \widehat {IAB} + \widehat {IBA} \\= \frac{{\widehat {BAC}}}{2} + \frac{{\widehat {ABC}}}{2}\;(1)\) Vì góc CBX và góc CAX là các góc nội tiếp của (O) cùng chắn cung nhỏ CX nên \(\widehat {CBX} = \widehat {CAX}\). Ta có: \(\widehat {IBX} = \widehat {IBC} + \widehat {CBX} = \frac{{\widehat {ABC}}}{2} + \widehat {CAX} \\= \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {CAB}}}{2}\;(2)\) Từ (1) và (2) ta có: \(\widehat {BIX} = \widehat {IBX}\) nên tam giác BIX cân tại X. Do đó, \(XI = XB\). Chứng minh tương tự ta có: \(XI = IC\). Vậy X là tâm của đường tròn ngoại tiếp tam giác BIC.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
