Giải bài 9.15 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2

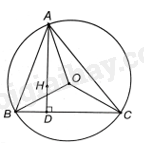
Đề bài

Cho tam giác ABC có trực tâm H và nội tiếp đường tròn (O). Chứng minh rằng:

a) \(\widehat {OBC} = {90^o} - \widehat {BAC}\);

b) \(\widehat {BAH} = \widehat {OAC}\).

Lời giải chi tiết

a) Vì góc nội tiếp BAC và góc ở tâm BOC của (O) cùng chắn cung nhỏ BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\) (1)

Tam giác BOC có \(OB = OC\) nên tam giác BOC cân tại O. Suy ra \(\widehat {OBC} = \widehat {OCB}\).

Do đó, \(\widehat {OBC} = \frac{{\widehat {OBC} + \widehat {OCB}}}{2} = \frac{1}{2}\left( {{{180}^o} - \widehat {BOC}} \right) = {90^o} - \frac{{\widehat {BOC}}}{2}\) (2)

Từ (1) và (2) ta có: \(\widehat {OBC} = {90^o} - \widehat {BAC}\).

b) Chứng minh tương tự câu a ta có: \(\widehat {OAC} = \frac{1}{2}\left( {{{180}^o} - \widehat {AOC}} \right) = {90^o} - \widehat {ABC}\;\left( 3 \right)\).

Gọi D là chân đường cao hạ từ đỉnh A của tam giác ABC.

Ta có: \(\widehat {BAH} = \widehat {BAD} = {90^o} - \widehat {ABD}\)  (vì tam giác ABD vuông tại D) (4).

Từ (3) và (4) ta có: \(\widehat {BAH} = \widehat {OAC}\).