Giải bài 9.18 trang 54 sách bài tập toán 9 - Kết nối tri thức tập 2Cho tam giác ABC vuông tại B nội tiếp đường tròn (O) và đường kính BD. Tính số đo của góc BAC, biết rằng (widehat {BAC} = 2widehat {CBD}). Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN Quảng cáo
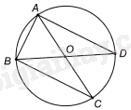
Đề bài Cho tam giác ABC vuông tại B nội tiếp đường tròn (O) và đường kính BD. Tính số đo của góc BAC, biết rằng \(\widehat {BAC} = 2\widehat {CBD}\). Phương pháp giải - Xem chi tiết + Chứng minh \(\widehat {CBD} = \widehat {CAD}\), \(\widehat {BAD} = {90^o}\). + Ta có: \(\frac{3}{2}\widehat {BAC} = \widehat {BAC} + \widehat {CBD} = \widehat {BAC} + \widehat {CAD} = {90^o}\), từ đó tính được góc BAC. Lời giải chi tiết
Xét đường tròn (O): + \(\widehat {CBD} = \widehat {CAD}\) (hai góc nội tiếp cùng chắn cung nhỏ CD) + Vì BAD là góc nội tiếp chắn nửa đường tròn nên \(\widehat {BAD} = {90^o}\). Ta có: \(\frac{3}{2}\widehat {BAC} = \widehat {BAC} + \widehat {CBD} \\= \widehat {BAC} + \widehat {CAD} = \widehat {BAD} = {90^o},\) suy ra \(\widehat {BAC} = \frac{2}{3}{.90^o} = {60^o}\).
|




















Danh sách bình luận