Giải bài 9 trang 75 vở thực hành Toán 9

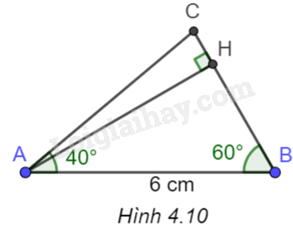
Đề bài

Cho tam giác ABC có \(\widehat A = {40^o},\widehat B = {60^o},AB = 6cm\). Hãy tính (làm tròn đến hàng đơn vị):

a) Chiều cao AH và cạnh AC;

b) Độ dài BH và CH.

Lời giải chi tiết

(H.4.10)

a) Trong tam giác vuông ABH vuông tại H, ta có: \(\sin \widehat {ABH} = \frac{{AH}}{{AB}}\) nên \(AH = AB.\sin \widehat {ABH} = 6.\sin {60^o} \approx 5\left( {cm} \right)\)

Xét tam giác ABC có \(\widehat {ACB} = {180^o} - \widehat {ABC} - \widehat {BAC} = {80^o}\)

Trong tam giác vuông ACH vuông tại H, ta có: \(\sin \widehat {ACH} = \frac{{AH}}{{AC}}\) nên \(AC = \frac{{AH}}{{\sin \widehat {ACH}}} = \frac{{6\sin {{60}^o}}}{{\sin {{80}^o}}} \approx 5\left( {cm} \right)\)

b) Ta có: \(\tan \widehat {ACH} = \frac{{AH}}{{CH}}\), nên \(CH = \frac{{AH}}{{\tan \widehat {ACH}}} = \frac{{3\sqrt 3 }}{{\tan {{80}^o}}} \approx 1\)

\(\tan \widehat {ABH} = \frac{{AH}}{{BH}}\), nên \(BH = \frac{{AH}}{{\tan \widehat {ABH}}} = \frac{{3\sqrt 3 }}{{\tan {{60}^o}}} = 3\left( {cm} \right)\).