Giải bài 8 trang 84 SGK Toán 8 tập 2– Chân trời sáng tạo

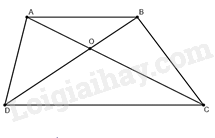
Đề bài

Cho hình thang \(ABCD\left( {AB//CD} \right)\), có hai đường chéo \(AC\) và \(DB\) cắt nhau tại \(O\). Biết \(AB = 8cm,CD = 20cm\). Khi đó \(\Delta AOB\backsim\Delta COD\) với tỉ số đồng dạng là

A.\(k = \frac{2}{3}\).                        

B. \(k = \frac{3}{2}\).                       

C. \(k = \frac{2}{5}\).                       

D. \(k = \frac{5}{2}\).

Lời giải chi tiết

Đáp án đúng là C

 

Vì \(ABCD\) và \(AB//CD\) nên \(\widehat {OAB} = \widehat {OCD}\) (hai góc ở vị trí so le trong)

Xét tam giác \(AOB\) và tam giác \(COD\) có:

\(\widehat {OAB} = \widehat {OCD}\) (chứng minh trên)

\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)

Suy ra, \(\Delta AOB\backsim\Delta COD\) (g.g)

Suy ra, tỉ số đồng dạng  \(k = \frac{{AB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\).