Giải bài 7 trang 53 sách bài tập toán 9 - Cánh diều tập 1Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\) Quảng cáo
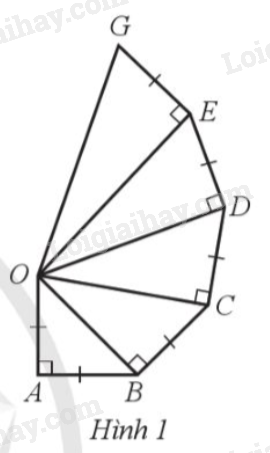
Đề bài Cho Hình 1 có \(OA = AB = BC = CD = DE = EG = 2cm\) và \(\widehat {OAB} = \widehat {OBC} = \widehat {OCD} = \widehat {ODE} = \widehat {OEG} = 90^\circ \). Tính độ dài các cạnh \(OB,OC,OD,OE,OG.\)
Phương pháp giải - Xem chi tiết Áp dụng định lý Pythagore lần lượt cho các tam giác vuông OAB, OCB, OCD, ODE, OGE. Lời giải chi tiết Áp dụng định lý Pythagore trong các tam giác vuông: - Tam giác OAB ta có: \(O{B^2} = O{A^2} + A{B^2} = {2^2} + {2^2} = 8\), do đó \(OB = \sqrt 8 cm.\) - Tam giác OCB ta có: \(O{C^2} = O{B^2} + C{B^2} = {\left( {\sqrt 8 } \right)^2} + {2^2} = 12\), do đó \(OC = \sqrt {12} cm.\) - Tam giác OCD ta có: \(O{D^2} = O{C^2} + C{D^2} = {\left( {\sqrt {12} } \right)^2} + {2^2} = 16\), do đó \(OD = 4cm.\) - Tam giác ODE ta có: \(O{E^2} = O{D^2} + D{E^2} = {4^2} + {2^2} = 20\), do đó \(OE = \sqrt {20} cm.\) - Tam giác OGE ta có: \(O{G^2} = O{E^2} + G{E^2} = {\sqrt {20} ^2} + {2^2} = 24\), do đó \(OG = \sqrt {24} cm.\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
