Giải bài 6 trang 53 sách bài tập toán 9 - Cánh diều tập 1Cho hình thang cân ABCD có AB // CD và \(AC \bot AD\). Tính độ dài cạnh AD, biết \(AB = 5cm,CD = 11cm.\) Quảng cáo
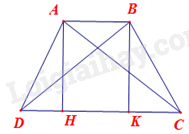
Đề bài Cho hình thang cân ABCD có AB // CD và \(AC \bot AD\). Tính độ dài cạnh AD, biết \(AB = 5cm,CD = 11cm.\) Phương pháp giải - Xem chi tiết Bước 1: Kẻ đường cao BH, CK. Bước 2: Chứng minh ABKH là hình chữ nhật, từ đó tính được HK. Bước 3: Chứng minh \(\Delta AHD = \Delta AKC\), từ đó tính được DH. Bước 4: Chứng minh , từ đó tính được AD. Lời giải chi tiết
Kẻ BH, CK lần lượt vuông góc với CD tại H, K do đó \(\widehat {AHK} = \widehat {BKH} = 90^\circ .\) Do \(BK \bot CD,AB//CD\) nên \(BK \bot AB\), suy ra \(\widehat {ABK} = 90^\circ \). Xét tứ giác ABKH, ta có \(\widehat {AHK} = \widehat {BKH} = \widehat {ABK} = 90^\circ \) nên ABKH là hình chữ nhật. Suy ra \(HK = AB = 5cm.\) Xét tam giác AHD và tam giác BKC ta có: AD = BC (ABCD là hình thang cân) AH = BK (ABKH là hình chữ nhật) \(\widehat {AHD} = \widehat {BKC}\left( { = 90^\circ } \right)\) Do đó \(\Delta AHD = \Delta AKC\)(cạnh huyền – cạnh góc vuông) Nên \(HD = KC = \frac{{CD - HK}}{2} = 3cm.\) Xét tam giác ACD và tam giác HAD có: \(\widehat {ADC}\) chung, \(\widehat {DAC} = \widehat {AHD}( = 90^\circ )\) Suy ra nên \(\frac{{CD}}{{AD}} = \frac{{AD}}{{HD}}\) hay \(A{D^2} = CD.HD\), do đó \(AD = \sqrt {CD.HD} = \sqrt {11.3} = \sqrt {33} cm.\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
