Giải bài 6 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 2

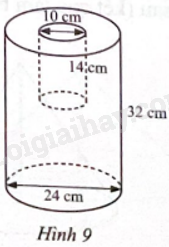
Đề bài

Từ một hình trụ có đường kính đáy 24 cm và chiều cao 32 cm, người ta khoét bỏ một hình trụ có đường kính đáy 10 cm và chiều cao 14 cm (Hình 9).

a) Tính thể tích của phần còn lại của hình trụ.

b) Người ta sơn toàn bộ các mặt của phần còn lại của hình trụ. Tính diện tích được phủ sơn (kết quả làm tròn đến hàng đơn vị của xăngtimet vuông).

 

Lời giải chi tiết

a) Thể tích của hình trụ ban đầu là:

\({V_1} = \pi {.12^2}.32 = 4608\pi \)(cm³).

Thể tích của hình trụ được lấy ra là:

\({V_2} = \pi {.5^2}.14 = 350\pi \)(cm³).

Thể tích của phần gỗ còn lại:

V = \(4608\pi  - 350\pi  = 4258\pi \)(cm³).

b) Diện tích toàn phần của hình trụ ban đầu:

\({S_1} = 2\pi .12.32 + 2\pi {.12^2} = 1056\pi \) (cm²)

Diện tích xung quanh của hình trụ lấy đi:

\({S_2} = 2\pi .5.14 = 140\pi \) (cm²).

Diện tích cần sơn:

S = S₁ + S₂ = \(1056\pi  + 140\pi  = 1196\pi  \approx 3757\)(cm²).