Giải bài 4 trang 103 sách bài tập toán 9 - Chân trời sáng tạo tập 2

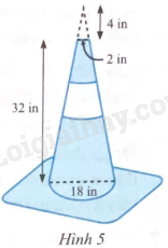
Đề bài

Một cọc tiêu có dạng hình nón bị cắt đi phần ở trên cũng có dạng hình nón như Hình 5.

a) Tính diện tích xung quanh của cọc tiêu theo đơn vị in² (không tính phần đế).

b) Tính thể tích của cọc tiêu theo đơn vị in³ (không tính phần đế).

(Làm tròn kết quả đến hàng đơn vị của in², in³).

 

Lời giải chi tiết

a) Độ dài đường sinh của hình nón bị cắt đi là: \({l_1} = \sqrt {{1^2} + {4^2}}  = \sqrt {17} \) (in)

Diện tích xung quanh hình nón bị cắt đi là: \({S_1} = \pi r{l_1} = \pi .1.\sqrt {17}  = \pi \sqrt {17} \) (in²).

Độ dài đường sinh của hình nón chưa bị cắt đi là: \({l_2} = \sqrt {{{36}^2} + {9^2}}  = 9\sqrt {17} \) (in)

Diện tích xung quanh hình nón chưa bị cắt đi là: \({S_2} = \pi r{l_1} = \pi .9.9\sqrt {17}  = 81\pi \sqrt {17} \)(in²).

Diện tích xung quanh của cọc tiêu là: \({S_2} - {S_1} = 81\pi \sqrt {17}  - \pi \sqrt {17}  \approx 1036\)(in²).

b) Thể tích của hình nón bị cắt đi là: \({V_1} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.1^2}.4 = \frac{4}{3}\pi \) (in³).

Thể tích của hình nón chưa bị cắt đi là: \({V_2} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.9^2}.36 = 972\pi \) (in³).

Thể tích của cọc tiêu là: \({V_2} - {V_1} = 972\pi  - \frac{4}{3}\pi  \approx 3049\)(in³).