Giải bài 3.35 trang 49 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

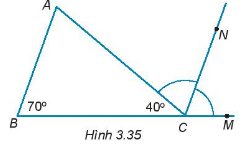
Đề bài

Cho hình 3.35. Biết CN là tia phân giác của góc ACM.

a) Chứng minh rằng \(CN//AB\).

b) Tính số đo của góc A.

Lời giải chi tiết

a)

Ta có: \(\widehat {ACM} + \widehat {ACB} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {ACM} + {40^0} = {180^0}\\ \Rightarrow \widehat {ACM} = {180^0} - {40^0}\\ \Rightarrow \widehat {ACM} = {140^0}\end{array}\)

Vì CN là tia phân giác của góc ACM nên

\(\widehat {ACN} = \widehat {NCM} = \dfrac{{\widehat {ACM}}}{2} = \dfrac{{{{140}^0}}}{2} = {70^0}\)

\( \Rightarrow \widehat {ABC} = \widehat {MCN} (= {70^0})\)

Mà 2 góc này ở vị trí đồng vị nên \(CN// AB\).

b)

Theo câu a) \(CN//AB\) nên \(\widehat A = \widehat {ACN}\) (2 góc so le trong). Mà \( \widehat {ACN}= {70^0}\) nên \(\widehat A =70^0\)