Bài 3 trang 156 Vở bài tập toán 8 tập 2

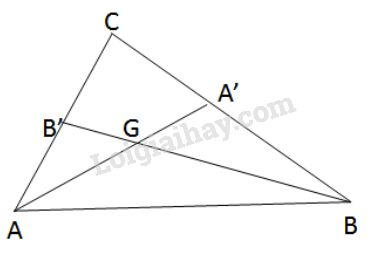
Đề bài

Trong tam giác \(ABC\) các đường trung tuyến \(AA’\) và \(BB’\) cắt nhau ở \(G\). Tính diện tích tam giác \(ABC\) biết rằng diện tích tam giác \(ABG\) bằng \(S.\) 

Lời giải chi tiết

(h.114) 

G là trọng tâm \(\Delta ABC\) (h.114) nên \(BB' = \dfrac{3}{2}BG\) 

Suy ra \({S_{ABB'}} = \dfrac{3}{2}{S_{ABG}} = \dfrac{3}{2}S\)  (1)  (Hai tam giác \(ABB'\) và \(ABG\) có chung đường cao hạ từ \(A\))

Ta lại có \({S_{ABC}} = 2{S_{ABB'}}\) (2) (Hai tam giác \(ABC\) và \(ABB'\) có chung đường cao hạ từ \(B\))

Từ (1) và (2) suy ra \({S_{ABC}} = 2.\dfrac{3}{2}S = 3S\)

Loigiaihay.com