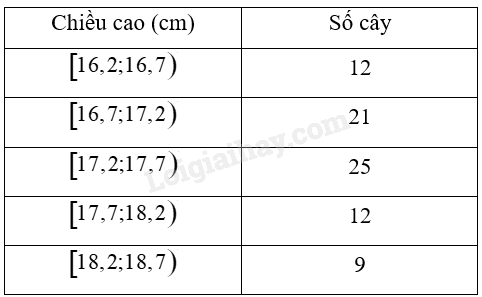
Giải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạoChiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau: Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm). Quảng cáo
Đề bài Chiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau:
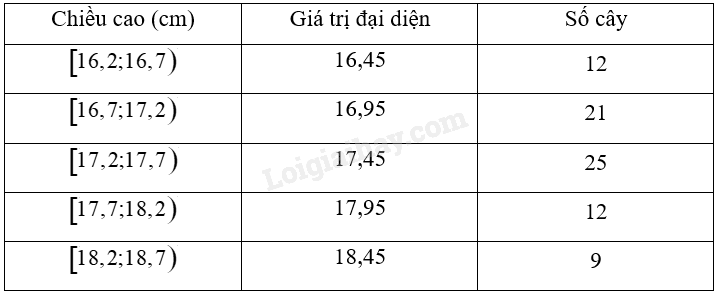
Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm). Phương pháp giải - Xem chi tiết ‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm: \(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\) ‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \). Lời giải chi tiết Ta có bảng sau:
Cỡ mẫu \(n = 12 + 21 + 25 + 12 + 9 = 79\) Số trung bình của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{12.16,45 + 21.16,95 + 25.17,45 + 12.17,95 + 9.18,45}}{{79}} \approx 17,3551\) Phương sai của mẫu số liệu ghép nhóm đó là: \({S^2} = \frac{1}{{79}}\left( {{{12.16,45}^2} + {{21.16,95}^2} + {{25.17,45}^2} + {{12.17,95}^2} + {{9.18,45}^2}} \right) - {17,3551^2} \approx 0,36\) Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S \approx \sqrt {0,36} \approx 0,6\).  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
