Giải bài 24 trang 32 SBT toán 10 - Cánh diều

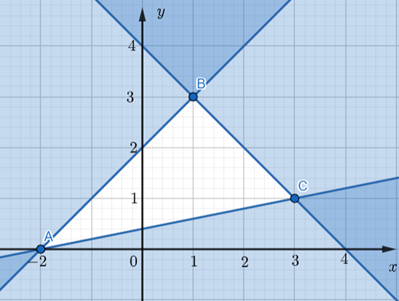
Đề bài

Giá trị nhỏ nhất của biểu thức  trên miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y \ge  - 2}\\{x + y \le 4}\\{x - 5y \le  - 2}\end{array}} \right.\)

A. -5                       B. -7                       C. 1                         D. 4

Lời giải chi tiết

Xác định miền nghiệm của hệ bất phương trình như sau:

- Vẽ ba đường thẳng:

Đường thẳng d1: x – y = – 2 đi qua các điểm có tọa độ (– 2; 0) và (0; 2).

Đường thẳng d2: x + y = 4 đi qua điểm có tọa độ (4; 0) và (0; 4).

Đường thẳng d3: x – 5y = – 2 đi qua các điểm có tọa độ (– 2; 0) và (3; 1).

Điểm O(0;0) thuộc miền nghiệm của BPT \(x - y \ge  - 2\) và BPT \(x + y \le 4\), nhưng không thuộc miền nghiệm của BPT \(x - 5y \le  - 2\).

Miền nghiệm của hệ bất phương trình là miền tam giác ABC (kể cả các cạnh) với

A(-2; 0), B(1; 3) và C(3; 1) như hình vẽ sau:

Tính giá trị biểu thức F = -2x+y tại các đỉnh của tam giác:

Tại A(– 2; 0), hay x = – 2 và y = 0 thì F = – 2.(– 2) + 0 = 4;

Tại B(1; 3), hay x = 1 và y = 3 thì F = – 2.1 + 3 = 1;

Tại C(3; 1), hay x = 3 và y = 1 thì F = – 2.3 + 1 = – 5;

=>  F đạt giá trị nhỏ nhất bằng – 5 tại x = 3, y = 1.

Chọn A