Giải bài 21 trang 81 SBT toán 10 - Cánh diều

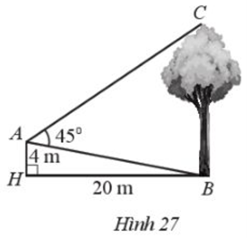
Đề bài

Một người đứng ở vị trí Atrên nóc một ngôi nhà cao 4 m đang quan sát đang quan sát một cây cao cách ngôi nhà 20 m và đo được \(\widehat {BAC} = {45^0}\) (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét)

Lời giải chi tiết

Áp dụng định lí Pytago cho ∆ABH vuông tại H ta có: \(AB = \sqrt {A{H^2} + H{B^2}}  = \sqrt {{4^2} + {{20}^2}}  \approx 20,4\) (m)

Xét ∆ABH vuông tại H  có \(\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{1}{5} \Rightarrow \widehat {ABH} \approx 11,{3^0}\)

Ta có: \(\widehat {ABH} + \widehat {ABC} = {90^0} \Rightarrow \widehat {ABC} = {90^0} - \widehat {ABH} = 78,{7^0}\) \( \Rightarrow \widehat {ACB} = {180^0} - (\widehat {ABC} + \widehat {CAB}) = 56,{3^0}\)

Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{20,4.\sin {{45}^0}}}{{\sin 56,{3^0}}} \approx 17,3\) (m)

Vậy chiều cao của cây là 17,3 m