Giải bài 2 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân. Quảng cáo
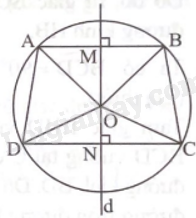
Đề bài Cho hình thang ABCD (AB // CD) nội tiếp đường tròn (O; R). Chứng minh ABCD là hình thang cân. Phương pháp giải - Xem chi tiết Vẽ đường thẳng d vuông góc với AB tại M và CD tại N. Chứng minh O cách đều các đỉnh của hình thang ABCD suy ra MN là trung trực của AB và CD. Khi đó, chứng minh \(\widehat {AOM} = \widehat {BOM}\); \(\widehat {DON} = \widehat {CON}\) suy ra \(\widehat {AOD} = \widehat {BOC}\). Chứng minh \(\Delta \)AOD = \(\Delta \)BOC suy ra AD = BC. Lời giải chi tiết
Qua điểm O vẽ đường thẳng d vuông góc với AB tại M và CD tại N. Ta có OA = OB = OC = OD = R, suy ra MN là đường trung trực của AB và CD. Tam giác AOB cân tại O có OM là đường trung trực nên OM cũng là đường phân giác, suy ra \(\widehat {AOM} = \widehat {BOM}\). Tương tự, \(\widehat {DON} = \widehat {CON}\). Khi đó, ta có: \(\widehat {AOM} + \widehat {AOD} + \widehat {DON} = \widehat {BOM} + \widehat {BOC} + \widehat {CON} = {180^o}\) suy ra \(\widehat {AOD} = \widehat {BOC}\). Xét \(\Delta \)AOD và \(\Delta \)BOC có: OA = OB \(\widehat {AOD} = \widehat {BOC}\) OC = OD Suy ra \(\Delta \)AOD = \(\Delta \)BOC (c.g.c). Dó đó AD = BC. Vậy ABCD là hình thang cân.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
