Bài 1.83 trang 41 SBT giải tích 12

Đề bài

Chứng minh rằng phương trình \(3{x^5} + 15x-8 = 0\) chỉ có một nghiệm thực.

Lời giải chi tiết

Hàm số \(f(x) = 3{x^5} + 15x - 8\) là hàm số liên tục và có đạo hàm trên \(\mathbb{R}\).

Có \(y' = 15{x^4} + 5 > 0,\forall x \in \mathbb{R}\)  nên hàm số đã cho luôn luôn đồng biến.

Mà \(f(0) =  - 8 < 0,f(1) = 10 > 0\)\( \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0\) nên tồn tại ít nhất một số \({x_0} \in (0;1)\) sao cho \(f\left( {{x_0}} \right) = 0\), tức là phương trình \(f\left( x \right) = 0\) có nghiệm.

Mà hàm số đồng biến trên R nên điểm này là duy nhất.

Vậy phương trình chỉ có một nghiệm duy nhất (đpcm).

Cách khác:

Hàm số \(f(x) = 3{x^5} + 15x - 8\) là hàm số liên tục và có đạo hàm trên \(\mathbb{R}\).

Có \(y' = 15{x^4} + 5 > 0,\forall x \in \mathbb{R}\)  nên hàm số đã cho luôn luôn đồng biến trên \(\mathbb{R}\).

Ta có:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {3{x^5} + 15x - 8} \right)\\
= \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^5}\left( {3 + \frac{{15}}{{{x^4}}} - \frac{8}{{{x^5}}}} \right)} \right] = - \infty \\
\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {3{x^5} + 15x - 8} \right)\\
= \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^5}\left( {3 + \frac{{15}}{{{x^4}}} - \frac{8}{{{x^5}}}} \right)} \right] = + \infty
\end{array}\)

Bảng biến thiên:

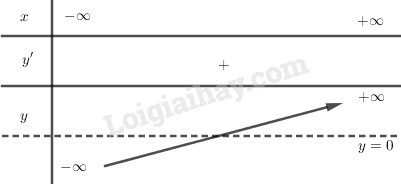
Từ bbt ta thấy đường thẳng y=0 luôn cắt đồ thị hàm số y=f(x) tại duy nhất 1 điểm hay pt đã cho có nghiệm duy nhất.

Loigiaihay.com