Bài 1.75 trang 39 SBT giải tích 12

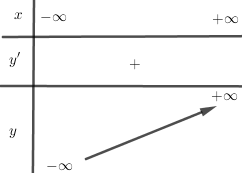
LG a

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với \(m = 1\).

Phương pháp giải:

- Tìm TXĐ.

- Xét chiều biến thiên.

- Vẽ đồ thị hàm số.

Lời giải chi tiết:

Với \(m = 1\) ta có hàm số \(y = 4{x^3} + x\).

TXĐ: \(D = \mathbb{R}\).

Ta có: \(y' = 12{x^2} + 1 > 0,\forall x \in \mathbb{R}\) nên hàm số đồng biến trên \(\mathbb{R}\) và không có cực trị.

Bảng biến thiên:

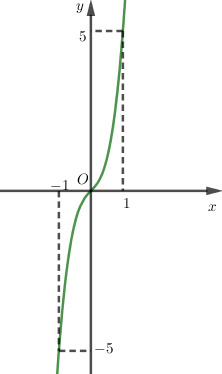
Đồ thị: Đi qua các điểm \(\left( {0;0} \right),\left( {1;5} \right),\left( { - 1; - 5} \right)\).

LG b

Viết phương trình tiếp tuyến của (C) song song với đường thẳng \(y = 13x + 1\).

Phương pháp giải:

Hai đường thẳng song song thi chúng có cùng hệ số góc.

- Tính \(y'\) và giải phương trình \(y' = k\).

- Tìm tọa độ tiếp điểm, từ dó suy ra phương trình tiếp tuyến.

Lời giải chi tiết:

Do tiếp tuyến song song đường thẳng \(y = 13x + 1\) nên \(k = 13\).

Ta có: \(12{x^2} + 1 = 13 \Leftrightarrow 12{x^2} = 12\) \( \Leftrightarrow x =  \pm 1\).

Với \(x = 1\) thì \(y = 5\), ta có tiếp tuyến \(y = 13\left( {x - 1} \right) + 5\) hay \(y = 13x - 8\).

Với \(x =  - 1\) thì \(y =  - 5\), ta có tiếp tuyến \(y = 13\left( {x + 1} \right) - 5\) hay \(y = 13x + 8\).

Vậy có hai tiếp tuyến phải tìm là \(y = 13x \pm 8\).

LG c

Xét sự biến thiên của hàm số (1) tùy thuộc giá trị của \(m\).

Phương pháp giải:

Biện luận nghiệm của phương trình \(y' = 0\), từ đó suy ra các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

Vì  \(y' = 12{x^2} + m\) nên :

+) Với \(m \ge 0\) ta có \(y' \ge 0\) với mọi \(x\).

Do đó hàm số (1) luôn luôn đồng biến khi \(m \ge 0\).

+) Với \(m < 0\) thì \(y' = 0 \Leftrightarrow x =  \pm \sqrt {\dfrac{{ - m}}{{12}}} \)

Từ đó suy ra:

+) \(y' > 0\) với \(x <  - \sqrt {\dfrac{{ - m}}{{12}}} \) hoặc \(x > \sqrt {\dfrac{{ - m}}{{12}}} \) nên hàm số đồng biến trên các khoảng \(\left( { - \infty ; - \sqrt {\dfrac{{ - m}}{{12}}} } \right),\left( {\sqrt {\dfrac{{ - m}}{{12}}} ; + \infty } \right)\).

+) \(y' < 0\) với \( - \sqrt {\dfrac{{ - m}}{{12}}}  < x < \sqrt {\dfrac{{ - m}}{{12}}} \) nên hàm số nghịch biến trên khoảng \(\left( { - \sqrt {\dfrac{{ - m}}{{12}}} ;\sqrt {\dfrac{{ - m}}{{12}}} } \right)\).

Loigiaihay.com