Giải bài 12 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1

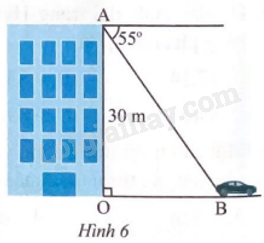
Đề bài

Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Từ điểm A trên đỉnh một toà nhà cao 30 m, một người nhìn thấy một ô tô đang dừng tại vị trí B dưới một góc nghiêng xuống là 55^o (Hình 6).

 

a) \(OB \approx 21m\)

b) \(AB = 47m\)

c) \(\widehat {{\rm{OAB}}}{\rm{ = }}{35^o}\)

D. \(\widehat {{\rm{OBA}}}{\rm{ = }}{35^o}\)

Lời giải chi tiết

a) Đúng vì xét tam giác OAB có \(\widehat {OAB} = {90^o} - {55^o} = {35^o}\)

Suy ra \( OB =\tan {35^o}.OA = \tan {35^o}.30 \approx 21m.\) 

b) Sai vì \(AB = \sqrt {O{A^2} + O{B^2}}  = \sqrt {{{30}^2} + {{21}^2}}  = 3\sqrt {149}  \approx 36,6m.\)

c) Đúng vì xét tam giác OAB có \(\widehat A = {90^o} - {55^o} = {35^o}\).

d) Sai vì \(\widehat {OBA} = {90^o} - \widehat {OAB} = {90^o} - {35^o} = {55^o}\).