Giải bài 1 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1Cho tứ diện ABCD. Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh \({G_1}{G_2}\) song song với các mặt phẳng (ABC) và (BCD). Quảng cáo
Đề bài Cho tứ diện ABCD. Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh \({G_1}{G_2}\) song song với các mặt phẳng (ABC) và (BCD). Phương pháp giải - Xem chi tiết Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P). Lời giải chi tiết
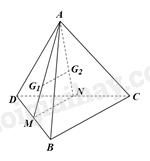
Gọi M, N lần lượt là trung điểm của DB, DC. Do đó, MN là đường trung bình của tam giác DBC. Suy ra MN//BC (1) Vì \({G_1}\) là trọng tâm của tam giác ADB nên \(\frac{{A{G_1}}}{{AM}} = \frac{2}{3}\). Vì \({G_2}\) là trọng tâm của tam giác ADC nên \(\frac{{A{G_2}}}{{AN}} = \frac{2}{3}\). Tam giác AMN có: \(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}}\left( { = \frac{2}{3}} \right)\) nên \({G_1}{G_2}//MN\) (2) (định lí Thalès đảo) Từ (1) và (2) ta có: \({G_1}{G_2}//MN//BC\). Vì \({G_1}{G_2}//BC\), \({G_1}{G_2}\) không nằm trong mặt phẳng (ABC), \(BC \subset \left( {ABC} \right)\) nên \({G_1}{G_2}\)//(ABC) Vì \({G_1}{G_2}//BC\), \({G_1}{G_2}\) không nằm trong mặt phẳng (DBC), \(BC \subset \left( {DBC} \right)\) nên \({G_1}{G_2}\)//(DBC).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
