Đề kiểm tra 15 phút - Đề số 2 - Bài 6 - Chương 3 - Hình học 9

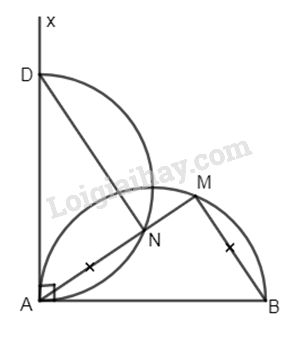
Đề bài

M  là điểm chuyển động trên nửa đường tròn đường kính AB. Trên tia AM lấy điểm N sao cho AN = BM. Tìm quỹ tích các điểm N.

Lời giải chi tiết

a) Phần thuận : Trên nửa mặt phẳng bờ AB có chứa nửa đường tròn ta dựng tiếp tuyến Ax. Trên Ax lấy điểm D sao cho AD = AB = 2R ( không đổi) nên D cố định.

Xét ∆ABM và ∆DAN có :

+) \(AB = AD\), ( cùng phụ với\(\widehat {MAB}\)),

+) \(BM = AN\) (gt).

Vậy \(∆ABM = ∆DAN\) (c.g.c) \(\Rightarrow \widehat {DNA} = \widehat {AMB} = 90^\circ \) ( AB là đường kính ).

Do A, D cố định nên N thuộc đường tròn đường kính AD.

Giới hạn: Khi M trùng A thì N trùng D.

Khi M trùng B thì N trùng A.

Do đó N chuyển động trên nửa đường tròn đường kính AD ( loại điểm A).

b) Phần đảo: Lấy điểm N’ bất kì thuộc nửa đường tròn đường kính AD. Nối N với A, đường AN’ cắt nửa đường tròn (O) tại M’. Ta phải chứng minh \(AN’ = BM’.\)

Thật vậy : Xét \(∆AM’B\) và \(∆DN’A\) có : \(\widehat {AM'B} = \widehat {DN'A} = 90^\circ ,\)\(AB = AD,\widehat {ABM'} = \widehat {DAN'}.\)

Vậy \(∆AM’B = ∆DN’A\) ( cạnh huyền – góc nhọn) \(\Rightarrow BM’ = AN’.\)

c) Kết luận: Quỹ tích các điểm N là nửa đường tròn đường kính AD ( loại điểm A).

 Loigiaihay.com