Câu 4.43 trang 109 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.43 trang 109 SBT Đại số 10 Nâng cao. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
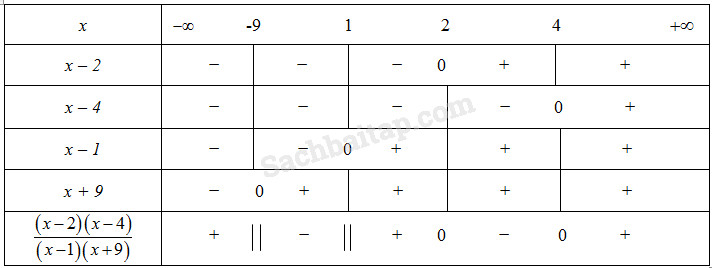
Xét dấu các biểu thức sau : LG a \(\dfrac{1}{{3 - x}} - \dfrac{1}{{3 + {x}}}\) Lời giải chi tiết: Biến đổi biểu thức về dạng \(\dfrac{{2{x}}}{{\left( {3 - x} \right)\left( {3 + {x}} \right)}}.\) Học sinh tự lập bảng xét dấu. Kết quả được biểu thức dương khi \(x < -3\) hoặc \(0 < x < 3\) ; biểu thức âm khi \(-3 < x < 0\) hoặc \(x > 3.\) LG b \(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}}\) Lời giải chi tiết: \(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}} = \dfrac{{\left( {{x} - 2} \right)\left( {{x} - 4} \right)}}{{\left( {{x} - 1} \right)\left( {{x} + 9} \right)}}\). Lập bảng xét dấu sau :
Vậy \(\dfrac{{{{x}^2} - 6{\rm{x}} + 8}}{{{x^2} + 8{x} - 9}} < 0\) khi \(x \in \left( { - 9;1} \right) \cup \left( {2;4} \right)\) \(\dfrac{{{{x}^2} - 6{x} + 8}}{{{x^2} + 8{x} - 9}} > 0\) khi \(x \in \left( { - \infty ; - 9} \right) \cup \left( {1;2} \right) \cup \left( {4; + \infty } \right)\) LG c \(\dfrac{{{{x}^2} + 4{x} + 4}}{{{x^4} - 2{{x}^2}}}\) Lời giải chi tiết: Biến đổi biểu thức về dạng \(\dfrac{{{{\left( {{\rm{x}} + 2} \right)}^2}}}{{{x^2}\left( {{{\rm{x}}^2} - 2} \right)}}.\) Từ đó, biểu thức đã cho sẽ dương khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; - \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right)\) và sẽ âm khi \(x \in \left( { - \sqrt 2 ;0} \right) \cup \left( {0;\sqrt 2 } \right).\) LG d \(\dfrac{{\left| {x + 1} \right| - 1}}{{{x^2} + {x} + 1}}\) Lời giải chi tiết: Ta có \(\dfrac{{\left| {x + 1} \right| - 1}}{{{x^2} + {x} + 1}} = \left\{ {\begin{array}{*{20}{c}}{\dfrac{{x}}{{{x^2} + {x} + 1}}\,khi\,x \ge - 1}\\{\dfrac{{ - x - 2}}{{{x^2} + {x} + 1}}\,khi\,x < - 1}\end{array}} \right.\) Dấu của biểu thức trên hoàn toàn phụ thuộc vào dấu của tử thức (vì \({x^2} + {x} + 1 > 0\) với mọi x). Vì vậy : \({{\left| {x + 1} \right| - 1} \over {{x^2} + x + 1}} < 0\) khi \(x \in \left( { - 2;0} \right)\) và \({{\left| {x + 1} \right| - 1} \over {{x^2} + x + 1}} > 0\) khi \(x \in \left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right).\) Loigiaihay.com
|




















Danh sách bình luận