Câu 16 trang 103 SGK Hình học 11 Nâng cao

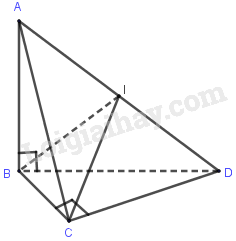
Đề bài

Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.

a. Tính độ dài AD.

b. Chỉ ra điểm cách đều A, B, C, D

c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).

Lời giải chi tiết

a. Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)

mà AC ⊂ (ABC) do đó CD ⊥ AC.

Trong tam giác vuông ABC ta có:

\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)

Trong tam giác vuông ACD ta có:

\(A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\)

Suy ra: \(AD = \sqrt {{a^2} + {b^2} + {c^2}} \)

b. Ta có: \(AB \bot BC\) và \(AB \bot CD\) suy ra AB ⊥ (BCD) do đó AB ⊥ BD.

Gọi I là trung điểm AD ta có:

+) Tam giác ACD vuông tại C có CI là đường trung tuyến ứng với cạnh huyền AD nên: \(IA = IC = ID = \frac{{AD}}{2}\left( 1 \right)\)

+) Tam giác ABD vuông tại B có BI là đường trung tuyến ứng với cạnh huyền AD nên: \[IA = IB = ID = \frac{{AD}}{2}\left( 2 \right)\]

Từ (1) và (2) suy ra: IA = IB = IC = ID

Vây I cách đều A, B, C, D.

c. Ta có: \(AB \bot \left( {BCD} \right)\) \( \Rightarrow BD\) là hình chiếu của \(AD\) trên \(\left( {BCD} \right)\).

Khi đó góc \(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left( {AD,BD} \right)} = \widehat {ADB}\).

Xét tam giác \(ABD\) vuông tại \(B\) thì \(\sin \widehat {ADB} = \dfrac{{AB}}{{AD}} = \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \( \Rightarrow \widehat {\left( {AD,\left( {BCD} \right)} \right)} = \arcsin \dfrac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Lại có \(DC \bot \left( {ABC} \right)\) \( \Rightarrow AC\) là hình chiếu của \(AD\) trên \(\left( {ABC} \right)\).

Khi đó góc \(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left( {AD,AC} \right)} = \widehat {DAC}\)

Xét tam giác \(ACD\) vuông tại \(C\) thì \(\sin \widehat {DAC} = \dfrac{{CD}}{{AD}} = \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\) \( \Rightarrow \widehat {\left( {AD,\left( {ABC} \right)} \right)} = \arcsin \dfrac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)

Loigiaihay.com