Bài 1 trang 125 SGK Hình học 11

LG a

Phép tịnh tiến theo vectơ $\overrightarrow v  = (2; 1)$.

Phương pháp giải:

Sử dụng biểu thức tọa độ của các phép biến hình.

Lời giải chi tiết:

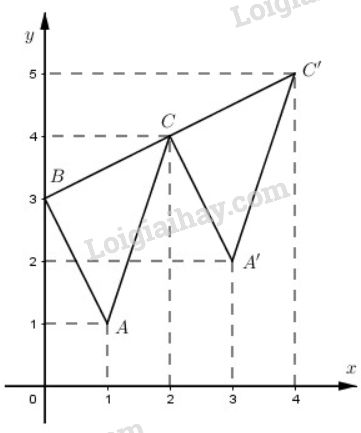
Trong phép tịnh tiến theo vectơ $\overrightarrow v  = \left( {2;1} \right)$ thì các đỉnh $A, B, C$ có ảnh là các điểm tương ứng $A’, B’, C’$.

Từ biểu thức tọa độ

$\left\{ \matrix{ x' = 2 + x \hfill \cr  y' = 1 + y \hfill \cr} \right.$

Ta có:

$A(1; 1) ⇒ A’(3; 2)$

$B(0; 3) ⇒ B’(2; 4)$

$C(2; 4) ⇒ C’ (4; 5)$

Tam giác $A’B’C’$, ảnh của tam giác $ABC$ trong phép tịnh tiến theo vectơ $\overrightarrow v$ là tam giác có ba đỉnh $A’(3; 2), B’(2; 4), C’(4; 5)$

Dễ thấy đỉnh $B’$ của $∆A’B’C’$ trùng với đỉnh $C$ của $∆ABC$.

Quảng cáo

LG b

Phép đối xứng qua trục $Ox$

Phương pháp giải:

Sử dụng biểu thức tọa độ của các phép biến hình.

Lời giải chi tiết:

Qua phép đối xứng trục $Ox$, biểu thức tọa độ là :

$\left\{ \matrix{ x' = x \hfill \cr  y' = - y \hfill \cr} \right.$

Do đó ta có: $∆ A’B’C’$ có các đỉnh $A’(1; -1), B’(0; -3), C’(2; -4)$

LG c

Phép đối xứng qua tâm $I(2;1)$.

Phương pháp giải:

Sử dụng biểu thức tọa độ của các phép biến hình.

Lời giải chi tiết:

Trong phép đối xứng qua tâm $I(2; 1)$, đỉnh $A→ A’$ thì $I$ là trung điểm của $AA’$. Gọi tọa độ $A’$ là $(x; y)$ thì:

$\eqalign{ & 2 = {{1 + x} \over 2} \Rightarrow x = 3 \cr  & 1 = {{1 + y} \over 2} \Rightarrow y = 1 \cr}$ 

$⇒ A’(3; 1)$

Tương tự, ta có ảnh $B’, C’$ của các đỉnh $B, C$ là $B’(4; -1), C’(2; -2)$

LG d

Phép quay tâm $O$ góc $90^0$.

Phương pháp giải:

Sử dụng biểu thức tọa độ của các phép biến hình.

Lời giải chi tiết:

Trong phép quay tâm $O$, góc quay $90^0$ thì tia $Ox$ biến thành tia $Oy$, tia $Oy$ biến thành tia $Ox$

Điểm $A(1; 1) → A’(-1; 1)$

           $B(0; 3) → B’(-3; 0)$

           $C(2; 4) → C’(-4; 2)$

LG e

Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục $Oy$ và phép vị tự tâm $O$ tỉ số $k = -2$

Phương pháp giải:

Sử dụng biểu thức tọa độ của các phép biến hình.

Lời giải chi tiết:

Trong phép đổi xứng qua $Oy$. $∆ABC$ biến thành $∆A_1B_1C_1$, ta có:

          $A(1; 1) → A_1(-1; 1)$

           $B(0; 3) → B_1(0; 3)$

           $C(2; 4) → C_1(-2; 4)$

Với phép vị tự tâm $O$ tỉ số $k = -2$ thì $∆A_1B_1C_1 → ∆A’B’C’$

           $A_1(-1; 1) → A’(2; -2)$

          $B_1(0; 3) → B’(0; -6)$

          $C_1(-2; 4) → C’(4; -8)$

Vậy trong phép đồng dạng đã cho thì $∆ABC$ có ảnh là $∆A’B’C’$ với  $A’(2; -2), B’(0; -6), C’(4; -8)$

 Loigiaihay.com