Bài tập 7 trang 156 Tài liệu dạy – học Toán 7 tập 1

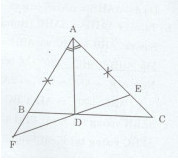
Đề bài

Cho tam giác ABC nhọn (AB < AC), phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AE = AB.

a) Chứng minh rằng $\Delta ADB = \Delta ADE$

b) Đường thẳng ED cắt đường thẳng AB tại F. Chứng minh rằng AF = AC.

c) Chứng minh rằng $\Delta DBF = \Delta DEC$

Lời giải chi tiết

a)Xét tam giác ADB và ADE có:

AB = AE (gt)

$\widehat {BAD} = \widehat {EAD}$   (AD là tia phân giác của góc BAC)

AD là cạnh chung.

Do đó: $\Delta ADB = \Delta ADE(c.g.c)$

b) Ta có:  $\Delta ADB = \Delta ADE$  (chứng minh câu a)

Suy ra: $\widehat {ABD} = \widehat {AED}$  và BD = ED

Xét tam giác AEF và ABC có:

$\widehat {EAF} = \widehat {BAC}$  (góc chung)

AE = AB (gt)

$\widehat {AEF} = \widehat {ABC}(\widehat {ABD} = \widehat {AED})$

Do đó: $\Delta AEF = \Delta ABC(g.c.g) \Rightarrow AF = AC$

c) Ta có: $\eqalign{  & \widehat {ABD} + \widehat {DBF} = {180^0}  \cr  & \widehat {AED} + \widehat {DEC} = {180^0} \cr}$    (hai góc kề bù)

Mà  $\widehat {ABD} = \widehat {AED}$  (chứng minh câu b) nên  $\widehat {DBF} = \widehat {DEC}$

Xét tam giác BFD và ECD có:

$\widehat {FBD} = \widehat {CED}(cmt)$

BD = ED (chứng minh câu b)

$\widehat {BDF} = \widehat {EDC}$  (hai góc đối đỉnh)

Do đó: $\Delta BFD = \Delta ECD(g.c.g)$

Loigiaihay.com