Bài tập 19 trang 97 Tài liệu dạy – học Toán 7 tập 2Giải bài tập Cho tam giác ABC nhọn có AB < AC, kẻ AH vuông góc với BC (H thuộc BC). Gọi M là điểm nằm giữa A và H, tia BM cắt AC ở D. Quảng cáo
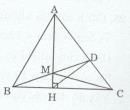
Đề bài Cho tam giác ABC nhọn có AB < AC, kẻ AH vuông góc với BC (H thuộc BC). Gọi M là điểm nằm giữa A và H, tia BM cắt AC ở D. a) Chứng minh BM < CM b) Chứng minh DM < DH Lời giải chi tiết
a) Ta có BH, CH lần lượt là hình chiếu của đường xiên AB, AC trên đường thẳng BC và AB < AC (gt). => BH < CH (quan hệ giữa đường xiên và hình chiếu) Mặt khác BH, CH lần lượt là hình chiếu của đường xiên BM, CM trên đường thẳng BC và BH < CH. => BM < CM (quan hệ giữa hình chiếu và đường xiên). b) \(\widehat {DMH} > \widehat {BHM} = 90^\circ (\widehat {DMH}\) là góc ngoài của tam giác BMH) ∆DMH có \(\widehat {DMH}\) tù =>\(\widehat {DMH}\) là góc lớn nhất trong ba góc => DH là cạnh lớn nhất trong ba cạnh (quan hệ giữa góc và cạnh trong một tam giác) Vậy DM < DH. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
