Bài 9 trang 135 SGK Toán 9 tập 2

Đề bài

Cho tam giác $ABC$ nội tiếp đường tròn $(O'$) và ngoại tiếp đường tròn $(O)$. Tia $AO$ cắt đường tròn $(O')$ tại $D$. Ta có:

(A) $CD = BD = O'D$ ;    (B) $AO = CO = OD$

(C) $CD = CO = BD$ ;      (D) $CD = OD = BD$

Hãy chọn câu trả lời đúng.

Lời giải chi tiết

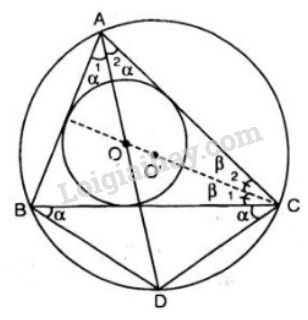
Vì $AC$ và $BC$ tiếp xúc với đường tròn $(O)$, $AD$ đi qua $O$ nên ta có AD là phân giác góc BAC (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)

Nên $\widehat {CA{\rm{D}}} = \widehat {BA{\rm{D}}} = \alpha$ 

Lại có $\widehat {CA{\rm{D}}}$ là góc nội tiếp chắn cung CD,  $\widehat {BA{\rm{D}}}$ là góc nội tiếp chắn cung BD

$⇒$ $\overparen{CD}=\overparen{DB}$ (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau)

 $⇒CD = DB$ (*) (hai cung bằng nhau căng 2 dây bằng nhau) 

Tương tự, $CO$ là tia phân giác của góc $C$ nên: 

$\widehat {AC{\rm{O}}} = \widehat {BCO} = \beta .$ 

Mặt khác: $\widehat {DCO} = \widehat {DCB} + \widehat {BCO} = \alpha  + \beta \, \,(1)$ (do $\widehat {BA{\rm{D}}} = \widehat {BC{\rm{D}}}$)

Ta có: $\widehat {CO{\rm{D}}}$ là góc ngoài của $∆ AOC$ nên

$\widehat {CO{\rm{D}}} = \widehat {OAC} + \widehat {OC{\rm{A}}} = \beta  + \alpha \, \, (2)$ 

Từ (1) và (2) ta có: $\widehat {OC{\rm{D}}} = \widehat {CO{\rm{D}}}$  

Vậy $∆DOC$ cân tại $D$ (2*)

Từ (*) và (2*) suy ra $CD = OD = BD.$

Chọn đáp án $D$.

Loigiaihay.com