Bài 6 trang 69 SGK Toán 9 tập 1

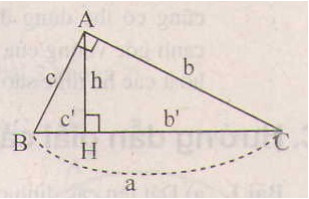
Đề bài

Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là \(1\) và \(2\). Hãy tính các cạnh góc vuông của tam giác này.

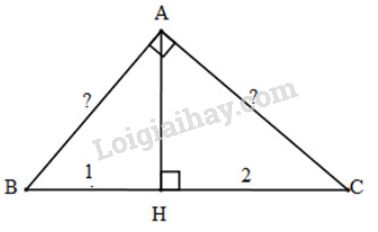
Lời giải chi tiết

Xét \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), \(BH=1,\ CH=2\). Ta cần tính \(AB,\ AC\).

Cách 1:

Ta có: \(BC=BH+HC=1+2=3\)

Áp dụng hệ thức lượng trong \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

        * \(AB^2=BH.BC \Leftrightarrow AB^2=1.3=3\)

                                         \(\Leftrightarrow AB = \sqrt 3\)

        * \( AC^2=CH.BC \Leftrightarrow AC^2=2.3=6\)

                                         \(\Leftrightarrow AC=\sqrt 6\)

Vậy độ dài hai cạnh góc vuông cần tìm là \(\sqrt 3\) và \(\sqrt 6\).

Cách 2:

Áp dụng hệ thức lượng trong \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

 

\(AH^2 = BH.HC=1.2=2 \Rightarrow AH =\sqrt{2}\)

Áp dụng định lí Pytago trong tam giác vuông ABH, ta được:

\(A{B^2} = B{H^2} + A{H^2} = {1^2} + {(\sqrt 2 )^2} = 3 \Rightarrow AB = \sqrt 3 \)

Áp dụng định lí Pytago trong tam giác vuông ACH, ta được:

\(A{C^2} = C{H^2} + A{H^2} = {2^2} + {(\sqrt 2 )^2} = 4 + 2 = 6 \Rightarrow AC = \sqrt 6 \)

Vậy độ dài hai cạnh góc vuông cần tìm là \(\sqrt 3\) và \(\sqrt 6\).